Из рис. 10.25 следует, что с ростом частоты ш граничные кривые Попова смещаются вниз. Можно также установить, что годограф G (/ш), как правило, убывает еще быстрее с ростом со.

В соответствии с рис. 10.24, г минимальное расстояние до прямой Попова равно

Рт = cos е. (10.48)

Поскольку cos 6g = , то согласно выражению (10.46) и (10.48) имеем

К(<7С0)2 + 1 Drg[C(jco)J, (град)

(10.49)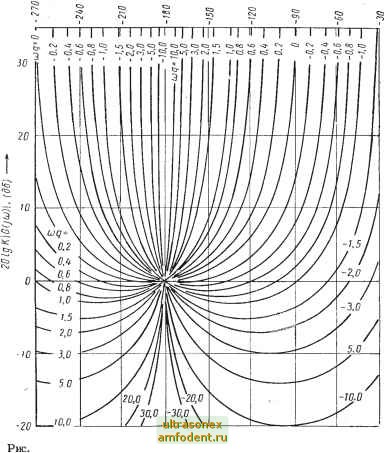

10.25. Граничные кривые Попова в логарифмическом масштабе

Если для некоторого значения да, G ( ш) < (gw), то ясно, что весь годограф лежит ниже этой граничной кривой. Из формулы (10.47) следует, что минимальное расстояние Рщ уменьшается с ростом частоты пропорционально ее первойстепени. Поскольку на практике убывание G (/ш) пропорционально первой степени или выше нее и если годограф G (/со) расположен ниже минимальных значений критических кривых в некотором диапазоне со, то взаимное расположение остается неизменным и для всех других значений со.

Годограф кривой 3G(/co) на рис. 10.26 всегда расположен ниже граничных кривых Попова при д = 1,2. Для того чтобы убедиться, что это утверждение верно и для области, не показанной на чертеже, заметим, что при со = 5 соответствующая точка годографа 3G (/ш) расположена ниже минимального значения кривой Попова дсо = 1,2X5= 6. Поскольку для данного

примера G уменьшается, как с ростом ш, то ясно, что и при ш> 5 годограф располагается ниже минимальных значений соответствующих кривых Попова. Следовательно, условие Попова выполняется для всех ш 0.

Как и раньше, проверку условия Попова можно упростить, если использовать плоскость KG * (/со). В соответствии с рис. 10.24, виг кривые на рис. 10.25 представлены в виде прямых Попова, показанных на рис. 10.4. Поэтому прямые Попова, изображенные на плоскости G *(/< )

arg[G(icj)] (град) --

1 I I I I I III )

-ипгсчГ (cf era

I I I I I I

о < оо q:i Ci CD era

<J- OQ C5

c= o C3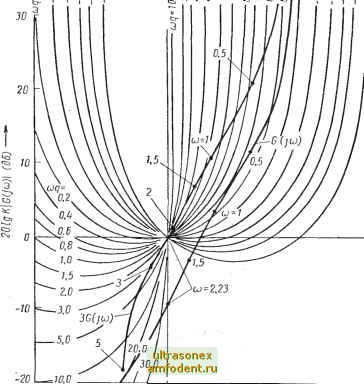

Рис. 10.26. Проверка условия Попова для системы из примера 10.14, позволяющая определить сектор Попова (и/е) с (0,3) такой, что при /С = 3 и 9= 1,2 годограф 3G Ош) расположен ниже граничных кривых Попова вида 1,2(0 для всех ш

(см. рис. 10.5), на плоскости с координатами [arg G* (ja), 20 Ig KG* (ja)] идентичны кривым

рис. Ш;-25;гДей&рамётр ад следует заменить на д.

Как только годограф KG* (ja) построен, можно сразу определить, ниже какой граничной кривой-Попбта;определяемой значением д, он расположен. Таким образом, в этом случае нет необхоДиШс!-!! применять метод последовательных приближений. Кроме того, дополнительная рабЬакеобхоДШая для проверки условия Попова на плоскости G (ja), не столь уж значительна и ока&Ыйае1-сяцеликом оправданной при синтезе коорректирующего устройства (упраж-

нение lO.lS. КйК- было отмечено в начале этого параграфа, подобный синтез провести на плоскости /?б*(/ф) о}сазывается затруднительным из-за соотношений (10.39).

10.9. КРАТКОЕ СОДЕРЖАНИЕ

Метод, предложенный В. М. Поповым для анализа абсолютной устойчивости, дает достаточные условия для устойчивости замкнутых систем, имеющих вид, показанный на рис. 10.1 при отсутствии входного сигнала. Основное достоинство этого метода заключается в том, что для его применения достаточно знать лишь частотные характеристики линейной части, а поэтому он пригоден для анализа систем высокого порядка.

Ограничения, которые приходится наложить на характеристики линейного и нелинейного элементов, рассматриваются в § 10.1. При этом нелинейность может обладать характеристиками типа пассивного или активного гистерезиса и (или) быть нестационарной, но существенно, что она должна принадлежать сектору, определяемому соотношениями (10.2). Линейный элемент должен иметь устойчивый выходной сигнал с коэффициентом затухания а (см. определение 10.3). Указанное требование ограничивает множество рассматриваемых линейных элементов, но в некоторых случаях оно может быть ослаблено (см. теорему 10.6), Предлагаемый метод позволяет анализировать системы с распределенными параметрами и запаздыванием.

Важными являются определение 10.4 понятия абсолютной асимптотической устойчивости выходной координаты и сигнала управления. Указанные свойства несколько слабее требования абсолютной устойчивости, которое вьшолняется лишь при дополнительных условиях (теорема 10.2).

Фундаментальное значение имеет теорема 10.1. Основное неравенство (10.19), определяемое через передаточную функцию линейной части G (/со), и некоторое действительное число q составляют существо этой теоремы. Для нестационарных нелинейностей это неравенство при = О позволяет дать простую геометрическую интерпретацию, в которой используются частотные годографы линейной части. Если же рассматриваются нелинейности при q =h О, то графическую проверку условий устойчивости целесообразнее осуществлять с применением модифицированной частотной характеристики линейной части G* (/со) [уравнение (10.21), (10.22), см. также рис. 10.5].

Класс систем, поддающихся анализу, можно расширить, если воспользоваться преобразованием, связанным со сдвигом полюсов передаточной функции линейной части системы; в этом случае появляется возможность проанализировать объекты, обладающие неустойчивостью. Кроме этого, такие системы можно анализировать, используя обобщенный круговой критерий [теорема 10.4 и условие (Ю.Зв)]. Последний способ особенно удобен при анализе систем с нестационарной нелинейной характеристикой, когда 9 = 0.

Дополнительные возможности, расширяющие применимость метода, дает преобразование, связанное со сдвигом нулей, оно позволяет снять некоторые ограничения, которым должен удовлетворять линейный элемент. Сущность этого приема содержится в теореме 10.6.

Все критерии, представленные в этой главе, можно без труда распространить на определение степени устойчивости системы. Такая возможность выявляется теоремой 10.3, которая обосновывает применение теоремы 10.1 и всех вытекающих из нее предложений для определения асимптотически устойчивого управления с коэффициентом затухания а. -

Возможность применения логарифмических частотных характеристик рассмотрена в § 10.8. При этом показано, как можно для анализа устойчивости использовать номограммы замыкания; круговой критерий для q = О непосредственно определяет соответствующие граничные кривые. Когда же 9 О, то и в этом случае оказывается возможным построить семейство