в процессе изложения устанавливается связь между классами допустимых характеристик нелинейного и линейного элементов. Именно метод Попова позволяет определить эту взаимосвязь, которая обеспечивает устойчивость и имеет важное значение при синтезе систем. Кроме того, излагая материал, мы используем такое определение устойчивости, которое соответствует инженерному взгляду на эту проблему. Все, что мы требуем, это асимптотическое стремление к нулю сигнала управления или выходного сигнала системы. Такое понимание устойчивости находит свое отражение в терминах асимптотически устойчивое управление и асимптотически устойчивый выходной сигнал , которые вводятся в разделе 10.2. Из этих свойств инженер, представляющий физическую структуру системы, может, если это необходимо, получить и другие характеристики устойчивости системы. Так, например, приводится теорема, с помощью которой устанавливается свойство абсолютной устойчивости, исходя из существования асимптотически устойчивого управления и ряда дополнительных условий.

Основные результаты этой главы сконцентрированы в одной теореме, которая служит основой для всех других формулировок критерия устойчивости. Эти критерии справедливы для систем с произвольно большим числом параметров при наличии и отсутствии запаздывания, а также для систем с распределенными параметрами. Ниже будет показано, что излагаемые методы не только позволяют исследовать факт устойчивости, но и определять степень устойчивости или демпфирование в системе. В заключение излагаются практические приемы анализа устойчивости и определение степени устойчивости, в том числе применение для этих целей логарифмических амплитудных и фазовых частотных характеристик.

Полученные результаты используются в следующей главе для установления факта устойчивости и единственности вынужденных решений. При доказательстве ряда теорем используются теорема Парсеваля, неравенства Шварца и Минковского, а также некоторые положения функционального анализа. При изложении материала данной главы мы опускаем математические подробности и отсылаем читателя к приложению III.

10. 1. НЕКОТОРЫЕ СВОЙСТВА ОСНОВНОЙ СИСТЕМЫ

Рассмотрим систему с обратной связью, которая показана на рис. 10.1. В ее состав входят нелинейный элемент и стационарная линейная часть. На практике большое число систем с однозначной нелинейностью можно привести путем ряда преобразований * к такой структурной схеме. Изучение устойчивости последней сводится к обобщенной задаче Лурье *; обобщен ность понимается в том смысле, что нелинейный элемент может быть нестационарным и (или) иметь гистерезисную характеристику определенного вида. Кроме того, линейный элемент может обладать запаздыванием или включать распределенные параметры. Вследствие этого уравнения системы целесообразнее всего представить в интегральной форме (см. § 3.9):

e{t) = eo{t)- g{t - x)u (<с) dx; (10.1а)

uit) = f[e{t),t], (10.16)

* См. § 9.5.

где g {f) = [G (s)] и -во (0 - соответственно, импульсная переход-

ная функция и реакция на начальные условия линейной части системы, а -е (t) - выходной сигнал системы.

Теперь рассмотрим ограничения, которым должны удовлетворять линейная и нелинейная части системы управления.

1. Нелинейный элемент

Функциональная связь между входом и выходом нелинейного элемента описывается соотношением (10.16). Некоторые частные виды нелинейных соотношений приведены в табл. 10.1. Разнообразие этих характеристик не

Таблица 10.1

Типы нелинейных элементов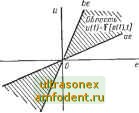

О б щ И й С Л у ч а й: W (О = [е (О, f]

Частные случаи:

u(t) = f [е (t)] - нелинейный однозначный, стационарный;

(О = / [в (t), t] - нелинейный однозначный, нестационарный;

и (t) = ff[e (i)] - нелинейный двузначный, стационарный;

и ({) = k (t) е (f) - линейный нестационарный; и (О = he {t) - линейный стационарный.

вызывает сомнения, однако все они должны располагаться внутри сектора, ограниченного двумя прямыми, проходящими через начало координат (см. рисунок). Другими словами, мы требуем, чтобы соблюдалось условие

для всех t, где а < Ь оо

Определение 1С рят, что (и/е) G [а, Ь]. Если выполняются условия (10.26), (10.2б) или (10.2г), то говорят, что (м/е) G [а, Ь), (и/е) G la, Ь) и {uje) G [а, Ы соответственно **.

* Напомним, что условие (10.2а) совпадает с ограничениями, которые налагаются на нелинейность в гипотезе Айзермана.

** Символ g означает принадлежит , а именно: с g С означает, что элемент с принадлежит множеству С. Обозначение [а, Ь \ определяет замкнутый интервал между а и Ы, т. е. интервал й и/е Ь. Обозначение (й, Ь) определяет открытый интервал между а и Ь или й <; {и/е) <; Ь. Обозначения (й, Ь ] и [й, Ь) определяют полуинтервалы и соответствуют следующим условиям: а <; (и/е) R (и/е) <; Ь.

u=ke-u

Если Ъ ограничено, то из ограниченности е (О li ввиду соотношений (10.2), следует ограниченность \u{t)\. Для того чтобы это условие выполнялось при любых (и/е) [а, оо], нужно требовать для всех t и каждого ограниченность значения и, т. е.

\u(t)]u<oo при 1 е (О I е. (Ю.З)

Условие (10.3) фактически выполняется для всех нелинейностей вида и {t) = 0 (е, t) и (м/е) 6 [а, оо], с которыми приходится иметь дело на практике. Например, для идеального реле и = sign е получим (w/e) 6 [О, оо] V. \ для любого е. Для нелинейности типа кубической параболы и =

- получим (ы/е) 6 [й, оо ] и

Как И Б ГЛ. 6, среди двузначных характеристик будем различать характеристики активного и пассивного гистерезиса. Для строгости изложения дадим следующие определения.

Определение 10.2. Стационарные характеристики гистерезисного типа можно определить, опираясь на понятие криволинейного интеграла. Говорят, что нелинейный элемент характеризуется пассивным гистерезисом, если условие.

О е, ег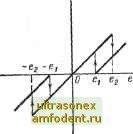

а) б)

Рис. 10.2. Нелинейные элементы:

а-с пассивным гистерезисом: б - с активным гистерезисом [случай а) можно преобразовать в 6) заменой переменных и - ке - и!

ude:

ude ------ ude - ude

Jr,2 Jr. Jri+ri2

Cl 0 0

Г(10.4а)

выполняется для любой пары точек и е, где контур Г определяет обход нелинейной характеристики в координатах {и,ё) при произвольном характере изменения е (), а и Г12 обозначают кривые (не замкнутые) на характеристике между точками О и к е- к соответственно. Говорят, что нелиней-ныйэлемент характеризуется активным гистерезисом, если условие

2 ее е, es

ude -

ude -

(10.46)

выполняется для любой пары точек и е.

Примеры двузначных характеристик показаны на рис. 10.2. На практике обычно встречаются характеристики пассивного типа. Однако характеристику пассивного типа можно преобразовать в характеристику с активным гистерезисом. Пример такого преобразования показан на рис. 10.2, б, который получен из рис. 10.2, в в результате преобразования и = ke - и (проделайте это самостоятельно). Мы будем использовать такое преобразование в дальнейшем при доказательстве ряда теорем об устойчивости.

2. Линейная часть

У стационарной линейной части системы связь между входом и выходом задается соотношением (10.1а) с использованием импульсной переходной функции g (f) - [G{s)] и реакции на начальные условия -ed-