Сохраняя начальную скорость хо на постоянном уровне и изменяя начальное положение Хю, можно получить семейство оптимальных кривых для ряда начальных состояний, которые Можно представить в виде, показанном на рис. 17.4.

Характеристики различных реальных конструкций систем управления пространственной ориентацией можно непосредственно нанести на график рис. 17.4. Степень приближения реальной конструкции к идеальной служит мерой обоснованности расчета этой конструкции.

В работе [147] предлагается ряд квазиоптимальных методов разработки реальной конструкции оптимальных систем управления.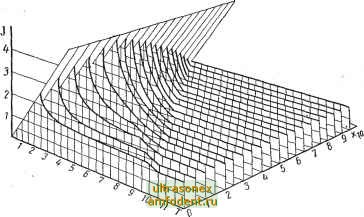

Рис. 17.4. Поверхность оптимальных характеристик для системы, рассматриваемой в примере 17.1, с = 1 и ОгХщЮ:

f - стоимость управления по расходу топлива; Т - продолжительность управления; Жю - начальное положение

17.3. КВАЗИОПТИМАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Если какая-либо задача формулируется в виде задачи оптимального управления, то ее решение в разомкнутом или замкнутом виде может показать, какое предельное качество будет достигнуто. Однако на практике вследствие целого ряда различных причин обычно трудно создать точную оптимальную систему управления. Приходится принимать ряд компромиссных решений, и таким образом получается субопти{лальная конструкция *.

Для определения обоснованности субоптимальной конструкции необходимо рассматривать насколько точно оптимальный расчет воплощен в реальной конструкции; насколько легко можно практически создать конструкцию путем использования существующих компонентов и насколько чувствительна конструкция к изменениям параметров и условий окружающей среды.

При оценке перечисленных выше факторов проявля.ется субъективность, и потому их трудно обсуждать достаточно обоснованно. Тем не менее две веские причины побуждают нас попытаться рассмотреть квазиоптимальные системы управления. Во-первых, субъективность является неизбежной реальностью на практике; однако даже в этих условиях существуют вполне определенные критерии в отношении выгодности их применения и качества, на основе которых плохие конструкции можно отделить от хороших. Во-вторых, несмотря на наличие большого числа опубликованных в литературе

* Под субоптимальной конструкцией понимается техническая реализация квазиоптимальной системы управления {Прим. ред.).

работ, посвященных вопросам оптимального управления, в значительном числе отраслей промышленности в основном применяются линейные методы расчета. Эти методы часто приводят к неудовлетворительному результату .при наличии больших сигналов. Такое положение можно исправить, если видоизменить расчет, придерживаясь в то же время основной сущности оптимального управления и учитывая особенности наличия больших сигналов.

Одной из существенно важных особенностей любой системы управления является ее нечувствительность к изменениям параметров. Вопрос о чувствительности или нечувствительности представляет собой тему все расширяющейся области исследований, которую мы не будем рассматривать детально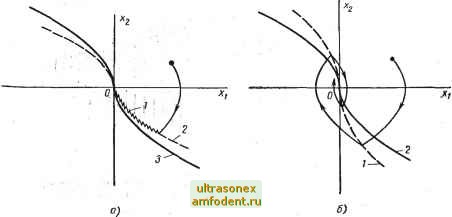

Рис. 17.5. Линии переключения для системы, рассматриваемой в примере 17.2:

а-скользящее движение; б-колебательное асимптотически устойчивое движение; /-скользящий режим; 2 - реализуемая линия переключения; 3 - расчетная линия переключения

Г46], [80]; тем не менее некоторое представление об основных идеях в этой области можно получить на следующем примере.

Пример 17.2. Для получения системы, способной обеспечить оптимальное управление каким-либо объектом, необходима аппаратура, создающая оптимальные линии или поверхности переключения. Этого можно добиться путем использования генераторов функций или каких-либо других средств. Предположим, что в аппаратуре для практического осуществления линии переключения допущена неточность или характеристики управляемого объекта изменяются в течение какого-то периода времени. В этом случае необходимо определить последствия этих факторов и принять меры для уменьшения чувствительности системы.

Рассмотрим объект управления, который описьшается дифференциальным уравнением второго порядка. Система, обеспечивающая оптимальное по быстродействию управление этим

объектом, показана на рис. 4.9. Для получения линии переключения-- I лга I Xg+t/xi

требуется генератор функций. Предположим теперь, что вследствие изменений параметров системы реализованная линия переключения вызывает раннее переключение. В результате получится скользящее движение вдоль линии переключения * (см. гл. 4), как показано на рис. 17.5, а. Кроме этого, если линия переключения такова, что имеет место позднее переключение, то результатом явится недостаточно демпфированное движение, как показано на рис. 17.5, б.

Из этих двух субоптимальных случаев один со скользящим движением в меньшей мере зависит от параметров системы и вследствие этого на практике целесообразнее рассчитывать

* Напомним, что на практике скользящее движение выражается в виде колебаний относительно линии переключения с высокой частотой и небольшой амплитудой, что обусловливается динамикой звеньев более высокого порядка в системе, которые не учитьшались при проектирова нии.

такую линию переключения, чтобы имело место скользящее движение вследствие раннего переключения.

Изложенное вьш1е можно распространить на квазиоптимальное управление другими, возможно, нелинейными объектами. Проиллюстрир5ем теперь на примере метод обоснованного квазиоптимального расчета упрощенного автопилота ракеты.

Пример 17.3, Рассмотрим двумерную модель ракеты, управление которой осуществляется с помощью стабилизатора [см. в гл. 5 примеры 5.6 и 5.8]. Уравнения движения представлены в виде зависимостей (5.15), которые можно записать:

ш(0 =4QC

(а. б);

(17.43а>

а (О = ш-

mV А

QCia, 6);

QCjv (а. 6),

(17.436) (17.43в>

где (0=6 - скорость изменения угла тангажа; а - угол атаки, а а д,- нормальное ускорение ракеты. Управляющим воздействием является угол отклонения руля 6. В качестве нелиней-

Рис. 17.6. Линейный автопилот ракеты:

од1(; - командный сигнал; i-усиление, зависящее от Q; 2, 3-линейные фильтры; 4 - привод руля; S - ракета; 6 - контур демпфирования; 7 - контур перегрузки; afj - выходной сигнал

ных функций выступают аэродинамические коэффициенты Сд (а, 6), Cj (а, 6) и Сдг (а, б), опре- деляемые на основе испытаний в аэродинамической трубе. Параметры А, t, J, т, g и Q определяются, как в примере 5.6. Следует отметить, что скоростной напор Q может изменяться в значительных пределах в диапазоне возможных режимов полета.

Обычно используемый метод расчета основан на локальной линеаризации, как было показано в примере 5.8, что приводит к уравнениям (5.20) и (5.21). Схема типового автопилота, полученная путем линейного расчета, показана на рис. 17.6. Здесь имеется внутренний контур демпфирования, в котором изменение угловой скорости 6 вращения корпуса ракеты, измеряемой скоростным гироскопом, компенсируется усилителем с коэффициентом усиления пропорциоиаль-ньш 1/Q и линейным фильтром. Полюсы или нули компенсирующей схемы можно, вероятно сделать зависящими от Q с тем, чтобы обеспечить возможность слежения за полюсами ракеты. Во внешнем контуре ускорение ракеты измеряется акселерометром и непосредственно используется в цепи обратной связи для вычитания его из входного сигнала. На этот .сигнал действует также линейная компенсирующая схема, усиление и динамика которой могут зависеть от Q.

При правильном выборе компенсирующих схем выходной сигнал ракеты будет достаточно следовать входному сигналу ракеты, по крайней мере при небольших сигналах, определяемых небольшими значениями а.

Известно, что ракеты, рассчитанные в соответствии с описанньш вьш1е методом, обладают хорошими характеристиками во многих некритических случаях. Однако, когда требуется обеспечить высокие характеристики, ракеты, рассчитанные в соответствии с линейными принципами, часто не отвечают предъявляемым к ним требованиям. . , ,

Покажем теперь, как некоторые основные положения оптимального управления можно использовать при расчете автопилотов с тем, чтобы улучшить характеристики ракеты при наличии больших сигналов.

К динамике ракеты предъявляются следующие основные требования:

1) маневренность, т. е. быстрота реакции на большие командные сигналы;

2) устойчивость или восстанавливаемость ракеты от воздействия не только больших командных сигналов-, но и от сильных возмущений;

3) нечувствительность больших сигналов относительно изменения аэродинамических факторов и условий окружающей среды (например, большое изменение в скоростном напоре Q);

4) простота конструкции.