б) найдите управляющую функцию и* как функцию состояния (т. е. в виде и* (х));

в) покажите, какие трудности вносит условие g (х) <У.

12.2. Не прибегая к математическим выкладкам, нарисуйте фазовый портрет для системы из примера (12.2), пользуясь нормальными координатами.

12.3. Найдите линию переключений для системы из примера 12.3.

12.4. Определите оптимальное управление по минимуму расхода топлива объектом с пере-

даточной функцией в виде -g-, т. е. Ху = х, х = и. Функционалом служит /= \u\(i) dt;

I и (О 1 1; JC (0) = JCo - произвольные начальные условия, а х (Г) = 0.

Покажите, то при Т f* управление (f), принимающее значения -1, О и имеет вид, изображенный на рис. 12.6, и обеспечивает меньшее значение /, чем управление вида ( = ±Ь. Здесь число Ь <С 1 положительно и выбрано таким, что одного переключения достаточно для перевода системы из состояния в состояние О за время Т. Минимизируйте функционал и найдите управление только для начальных точек, находящихся на оси Ху.

12.5. Покажите, что для некоторых значений f* <СТ<С оз. существует бесконечное множество оптимальных управлений для системы, рассмотренной в примере 12.5 (указание: рассмотрите управление, которое не требует переключения полярности и* (f)).

12.6. Можно ли при решении задачи оптимального быстродействия перевести систему из произвольных начальных условий в начало координат, если заданы: уравнение системы у+ (а -Ь Ь) у + аЬу = и (f) к ограничения и (f) ]< 1; а< 0; Ь < О?

12.7. Рассмотрите оптимальное управление по быстродействию для объекта с передаточ-

ной функцией , когда Xi = х; х = Xg, х = и, при условии м I [/. Если начало координат представляет собой конечное состояние системы, определите уравнения для линии и поверхности переключения.

12.8. Докажите, что уравнение (12.15) определяет оптимальную передаточную функцию Я* (s) для класса задач, рассмотренных в § 12.2.

12.9. Для объекта --- -- найдите моменты переключения и оптимальное уп-

Р (Р -г 1) (Р -г-й)

равление, которое обеспечивает при движении из начального положения с координатами (2, 1, 3) в начало координат минимум времени переходного процесса. При этом используйте нор мальные координаты.

Допущение: (Q1, управление релейное.

12.10. Для объекта найдите оптимальный корректирующий фильтр (§ 12.2),

который минимизирует функционал (е (t) -\- tfi (i)) dt при условии, что входной сигнал r(t) =

= е~. Положите, что при = О все начальные условия нулевые, . .

12.9. УКАЗАНИЯ НА , ЛИТЕРАТУРУ

Материал § 12.2 изложен в работах [32], [150]. Синтез оптимального по быстродействию управления для линейных систем второго порядка изложен в работах [63] и [189]. Синтез систем высокого порядка с действительными собственными значениями рассмотрен в работе [167], а синтез систем третьего порядка - в работе [21 ]. В работе Бушау [29] излагаются вопросьг, связанные с релейным управлением объектами с колебательными свойствами.

ГЛАВА 13

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

Вариационное исчисление является областью математики и связано с нахождением траекторий, которые максимизируют или минимизируют заданныйфункционал. Не вызывает никакого сомнения, что современные методы оптимального управления такие, как принцип максимума Понтрягина и динамическое программирование Беллмана, основанные на различных положениях, в значительной степени навеяны классическим вариационным исчислением.

Пцеи вариационного исчисления легко усвоить, изучая семейства траекторий в пространстве состояний. На этой основе можно получить целый ряд интересных результатов, касающихся определения максимумов и минимумов функций; именно простота и изящность получаемых результатов привлекают внимание к принципам вариационного исчисления. Понимание математического аппарата вариационного исчисления облегчает изучение принципа максимума и динамического программирования.

В данной главе исследуются некоторые положения вариационного исчисления, которые непосредственно могут быть применены в задачах оптимального управления. Изучив простейшие принципы, мы сразу приступаем к анализу уравнений Эйлера-Лагранжа и других необходимых условий оптимальности. Из анализа этих уравнений и граничных условий удается глубже понять характерные особенности задач оптимального управления.

Если система управления нелинейная и требует решения двухточечной краевой задачи, то эти решения обычно отыскиваются методом проб и ошибок. Только для линейной системы, когда показатель качества является интегралом от суммы квадратов переменных состояния и управляющего воздействия, можно получить аналитические решения.

Вариационное исчисление помогает определить необходимые условия оптимальности для достаточно широкого круга задач управления. Например, метод Валентайна позволяет рассматривать системы с ограничениями на управляющее воздействие. Следовательно, вариационное исчисление является достаточно мощным методом, хотя специфика понятий и приемов часто затеняет существо задачи. Более прямыми методами решения оптимальных задач являются принцип максимума и метод динамического программирования.

13.1. УРАВНЕНИЯ ЭЙЛЕРА-ЛАГРАНЖА И ДРУГИЕ НЕОБХОДИМЫЕ УСЛОВИЯ ЛОКАЛЬНОГО МИНИМУМА

Вариационное исчисление, строго говоря, не позволяет прямо находить оптимальное решение. Оно лишь определяет необходимые условия, которым должна удовлетворять оптимальная траектория, и, следовательно, позволяет

отбросить множество неоптимальных траекторий. Иногда остается единственная траектория, которая и является оптимальной.

Вариационное исчисление позволяет получить ряд важных результатов, которые применительно к оптимальному управлению можно истолковать следующим образом. Предположим, что необходимо найти оптимальное управление ю* (f), которое переводит систему x = f{x, ю) в течение интервала времени [t, t] из первоначальной точки х (ti) = л; в конечную точку

лг (4) = лга, минимизируя ) при этом .

функционал

/= I L{x, u)dt.

(13.1)

Некоторые, хотя и нестрогие выводы можно сделать, рассматривая траекторию X, изображенную в функции от t на рис. 13.1. Каждому выбору и (f) на интервале [ty, t] ставится в соответствие траектория X {f), но все траектории должны

начинаться из точки х = X {ty) и кон-д

чаться в точке лгз = лг (t). СледователЁ-

но, траектория лг (t), рис. 13.1, должна быть как она начинается в лг, в лгз- Как следует из гл.

показанная,- на исключена, так но не кончается 12, требование.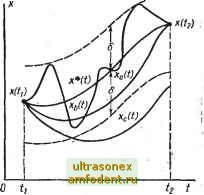

Рис. 13.1. Кривая Xa(f), удовлетворяющая условиям II JC* (t) -Ха (0116

и II ir* (О - Jca (t) <б для tt лежит в слабой б-окрестности JC* (f); кривая Хд (О, удовлетворяющая условиям II X* - JC6 (О II S и IIX* - хь (О >> для некоторых t расположена в сильной б-окрестности х* (t)

ЧТО все траектории начинаются в точке Ху, еще не означает, что все они заканчиваются в точке лга.

Допустим, что каким-то способом мы сумели найти ряд тра.екторий, которые соединяют ЛГ1 с ЛГз и удовлетворяют другим условиям нашей задачи оптимального управления. Далее следует найти среди этих траекторий такую, которая дает наименьшую величину функционала Оказывается, определение траектории, доставляющей абсолютный минимум функционала, представляет очень сложную задачу. Намного проще определение траектории, соответствующей локальному минимуму функционала. Последнее условие исходит из понятия близости двух траекторий, которое мы сейчас и рассмотрим.

Предположим, имеется кривая лг* (t), определенная в соответствующем пространстве состояний. Тогда будем говорить, что кривая лг (Щрасполо-жена в слабой б-окрестности кривой лг* (t), если для величин лг (t) и ЛГ1 (t) выполняются условия: лг* () - лг (О = б; [лг*()-Ji;i(0ll=6 (см. кривую Ха (О на рис. 13.1). Будем также называть кривую лг (t) принадлежащей сильной б-окрестности лг* (t), если вьшолняется только первое условие, т. е. II лг* (t) - лг (t) II б (см. кривую лг, (t) на рис. 13.1).

Говорят, что траектория лг* (t) обеспечивает слабый (сильный) локальный минимум, когда имеется такая слабая (сильная) окрестность траектории лг* (t), что значение функционала /, определенного вдоль траектории лг* (t), меньше, чем его значение вдоль любой другой траектории, находящейся в этой окрестности. Отсюда видно, что сильный минимум обязательно

Так как min / = -max (-то достаточно рассмотреть только задачи минимизации.