то начало координат системы (9.28) равномерно асимптотически устойчиво в целом *.

Рассмотрим вкратце идеи, положенные в основу доказательства этих теорем. Прежде всего отметим, что в случае, когда V - нестационарная функция, условия F > О для всех л: =f О и произвольного t недостаточно, чтобы гарантировать свойство асимптотической устойчивости даже, если V <с0 для всех X =h.O п произвольного t. Действительно, если в уравнении (9.29) член , являясь отрицательным, превосходит по модулю член

(grad Vy f, то производная ~ оказывается отрицательной.

Поскольку именно член (grad Vyf определяет движение системы, то может оказаться, что V будет меньше нуля, в то время как изображающая точка будет находиться вне некоторой ограниченной области

Если же V (х, t) превосходит некоторую скалярную функцию переменной \\х\\, удовлетворяя тем самым неравенству (9.27), то все сказанное выше уже не может иметь места. Действительно, при произвольном е всегда можно найти б (е, zo) <j е такое, что V {Xq, t) <5 Ф (е). Отсюда следует просто устойчивость и асимптотическая устойчивость, поскольку при V функция V не может превзойти Ф (е). Более того, свойство асимптотической устойчивости не зависит от Xq, и, следовательно, начало координат эквиасимптотически устойчиво.

Для равномерной устойчивости необходимо, чтобы V {х, t) была ограничена сверху функцией р (л:). Тогда для произвольного е >0 можно подобрать такое б, что будет выполняться р (б) <Н Ф (е). Отсюда следует, что Ф (е) > р (б) V (ЛГо, /о) {X (О, t) Ф( л: (О ) для всех t > t.

Равномерная устойчивость при этом очевидна, поскольку выбор величины б не зависит от t.

Значительно сложнее доказать, что при выполнении условий теоремы 9.11 изображающая точка x{t) стремится к началу координат равномерно полго и to- Это доказательство, принадлежащее Массера [134], приводится ниже **.

В области М выберем такие числа с и б, что р (б) <з Ф (с). Это означает, что при IIЛГоII бц б (с) определяет границу, общую для всех Цл: (/) .. Допустим, что нам задана величина р, ЦлГоЦ. тогда можно найти р. >0 такое, что р (р,) <; Ф (р,). Поскольку р, р, = с, то непрерывная функция G (z) из теоремы 9.10 имеет минимум в точке z: Р- z с. Обозначим эту точку через с. Теперь покажем, что величину Т в определении равномерной асимптотической устойчивости можно выбрать равной Т = -f .

Прежде всего заметим, то существует момент времени t: to <i f <1 <. ti = to + Т, когда IIл: (f) II = p. По определению л:о>р. Если X (Oil > м- для всех t; to <С t<C t, то

0{li)V{x{t,y, t,)ViXo, to)-{tx-to)c.

Поскольку p (6J V (Xo, to) я T = то

0 <Ф ill) p (8,) - Тс =0.

* Напомним, что в § 5.6, где введено это понятие, оно объединяло следующие свойства:

1) равномерную устойчивость в смысле Ляпунова по переменным Хо и ;

2) равномерную ограниченность, т. е. для любого /> О существует В, зависящее лишь от г, такое, что условие Хо - Хег влечет за собой \\х (t) - JCe В для всех ttg-,

3) предположим что любая траектория в фазовом пространстве стремится к Хе при / оо равномерно по переменным х, и t,-

** См. также работу [66], стр. 65.

Полученное противоречие приводит к выводу, что Цл:(f) =л: = Рассмотрим траекторию, которая начинается в момент времени f. При этом имеем неравенство

Ф(л:(л:, Г; t)\\)Vix(x, Г; t), t)V{x, 0<Р(Ю<Ф(),

которое означает, что л: (лго, oJ О II < Для всех tto+T. Таким образом доказано свойство равномерной асимптотической устойчивости.

После этого сравнительно просто показать, что устойчивость в целом выполняется, если Ф (]л:)оо, когда ЦлгЦ-оо.

Следует вновь подчеркнуть, что для систем с переменными параметрами, как правило, необходимо выбирать функцию V, не зависящую от времени. Совершенно ясно, что в этом случае для равномерной асимптотической устойчивости требуется лишь положительная определенность функции V в стационарном смысле, т. е. F (л:) > 0; л: =f О и V (0) = 0. Кроме того, функция V, которая остается функцией времени, должна удовлетворять условию (9.30)

Пример 9.12. Рассмотрим дифференциальное уравнение с переменными параметрами следующего вида [126]:

x + p{t)x + g{t)x=0

% = - а > л;а = -9(0% -Р(02-

(9.32)

Предположим, что функции р (Q а д {f) - непрерывные функции своего аргумента и Я (t) 0. Требуется наложить ограничения на функции р (t) и q (t), чтобы обеспечить асимптотическую устойчивость начала координат. Эти ограничения мы найдем двумя способами, используя в первом случае стационарную, а во втором - нестационарную функцию Ляпунова.

Случай 1. Определим функцию

(9.33)

если Gi>- О и ааУ 1, то функция V определенно положительна. Более того,

-=~\я (О ?+h ? (О+Р (О - i] 12 + hp (t) -1] ) =

<hP (t) - 1 --

(p(0+fl2g(0- i)

(9.34)

Поскольку q [t) ?i > 0, то при условии, что коэффициент при х положителен, функция V будет определенно отрицательной. Таким образом, получим условие

[p(0+(0-ai]

2Р (О - 1 -

4q(t)

где S - произвольное положительное число.

В результате преобразований соотношение (9.35а) можно представить в виде

[р (О - aq (t) - aV - 4 [аа - 1 - е) ? (/) О

и, кроме того, из соотношения (9.35а) следует, что

Pit):

, , . , [Р (О + (hP. it) - fii] I n 4(0

(9.35a)

(9.356) (9.36)

Уравнения (9.35) и (9.36) совместно с условием (OiO определяют область (рис. 9.7), заштрихованную на плоскости переменных ((?,р). Внутри нее выполняется условие асимптотической устойчивости; область ограничена параболой

[р - aq - Gi)2 - 4 (aiG2 - 1 - е) ? = О (9.37)

и прямой (? =

Если выполняются уеловия

0<Pip(OP2; 0< 9i9(0<?2. (9.38)

где Pi, pg, 9i и - постоянные величины, то не представляет труда построить область устойчивости на плоскости переменных (р, q), задаваясь параметрами и а- Поскольку от этих параметров зависит лишь знакоопределенность функции V, то их можно исключить, построив максимально возможную область устойчивости.

Рассмотрим параболу (рис. 9.8), которая проходит через точку с координатами (q, pJ, определяемыми нижней границейэтих переменных. Допустим, что кривая проходит и через точку (2, pj) с той же ординатой Pj и при этом д (?2 Подставляя эти координаты в уравне- Р2* ние (9.37), получим два уравнения относительно

Рис. 9.7. Заштрихованная область на плоскости параметров (р, (?) определяет область асимптотической устойчивости и ограничена параболой вида (9.37) и прямой 9 = ft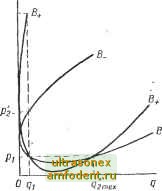

Рис. 9.8. Геометрическая интерпретация способа отыскания максимально возможной области устойчивости на плоскости переменных (р, q)

параметров Gj и а,. Исключая параметр а, находим Gg, а затем выражаем Gj через Gj. При этом возможны две пары чисел (Оц., G2+), (Gi , G2 ), и следовательно, две параболы проходят через одни и те же точки, координаты которых удовлетворяют условиям

2± =

!+ =

Pi ± Vp\ ~ Ki) (1 -f е)

1-fe

(9.39а)

(9.396)

Поскольку параметр aj является действительным числом, то из соотношения (9.39а) следует, что должно выполняться условие

Р? \У2 ~ Vif (1 + е). (9-40)

Теперь определим ординаты парабол при фиксированной абсциссе q. Ординаты Р2, зависящие от q, pj, q и е, определяются из уравнения (9.37) и равны

1 -eVii

= РН

Р2 ( ь Рь 92, е)+ = Pi + 4 Vio

(p,±ypl~-{Vq;~Vq,)\l + 4 (9.41)