коэффициент усиления реле будет регулировать величину предельного коэффициента усиления. Это значит, что установившаяся амплитуда колебаний будет функцией параметров объекта управления *. Последнее хорошо видно из рис. 7.12, б и е.

Рассмотрим поведение колебательного сервомеханизма с другой точки зрения. Предположим, что, спустя некоторое число циклов, входной сигнал г (t) изменился, но незначительно. Тогда приближенно можно считать, что г (t) представляет постоянную величину. Если бы сигнал г (/) поддерживался равным R, то сигнал y(t)=R. Таким образом, если г (t) изменяется достаточно медленно, то сигнал на входе реле может быть представлен в виде

+ бо sin cOq/, где eje(, мало. В этом случае соотношения (7.42) будут справедливыми. Из соотношения (7.42а) нетрудно получить эквивалентную передаточную функцию по постоянной

составляющей в виде Ns (fig, (2U/n.es) arcsin (ejea); причем зависимость постоянных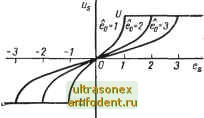

Рис. 7.13. Зависимость между постоянной составляющей выходного и входного сигналов для идеального реле при переменных амплитудах колебательной составляющей во

G(p)--

p(p+a)

p(p*a)

Рис. 7.14. Структурная схема системы управления примера 7.4:

а - для низкочастотной составляющей; б -для высокочастотной составляющей

составляющей выхода и входа показана на рис. 7.13. Из рисунка видно, что с ростом переменной составляющей характеристика реле линеаризуется.

Обозначая эквивалентную передаточную функцию по постоянной составляющей через iVj, а по переменной составляющей через Л , получим

I К бо

(7.51а)

<

<1; es<0,8eo.

(7.516)

Две эквивалентные структурные схемы системы - одна по переменной составляющей, другая по постоянной составляющей показаны на рис. 7.14, и и б, где - постоянная составляющая входного сигнала, а {t) - медленно меняющаяся компонента.

Черавенство (7.156) показывает еще раз, что при определенных значениях отношения \es\leo эквивалентное усиление по постоянному сигналу всегда меньше, чем по переменной составляющей, которое, в свою очередь, характеризует предельное усиление системы. Тем не менее эквивалентное усиление по постоянному сигналу никогда не может более, чем на 6 дб, отличаться от предельного усиления.

Частота автоколебаний в данном случае изменяется незначительно (Прим. ред.у

в заключение отметим следующие основные достоинства колебательного сервомеханизма:

1) эквивалентная система для постоянного сигнала всегда устойчива; более того, она всегда будет работать немного ниже предела устойчивости;

2) небольшие скачки ступенчатого входного сигнала отрабатываются в течение периода актоколебаний.

Иногда автоколебания сервомеханизма являются нежелательными, то тогда надо стремиться сделать амплитуду актоколебаний как можно меньшей. Может оказаться, что колебательный сервомеханизм представляет собой подсистему большей системы и колебания его выходного сигнала будут отфильтровываться элементами большей системы. Тогда в выходном сигнале большей системы эти колебания не будут наблюдаться. И, наконец, во многих случаях малая переменная составляющая может улучшить работу системы, так как она уменьшает влияние нелинейностей, таких, как люфт и сухое трение *.

Как правило, переменная составляющая поступает в систему извне. Высокочастотный сигнал на входе реле оказывает линеаризующее действие, причем усиление низкочастотного сигнала зависит от амплитуды высокочастотного управляющего сигнала. Таким образом, имеется простой способ получения требуемого усиления системы.

7.6. Краткое содержание

Эквивалентная передаточная функция для двухчастотного входного сигнала представляет собой логическое расширение того же понятия для случая одночастотного входного сигнала. Она определяет эквивалентное усиление- по двум различным составляющим сигнала, который проходит через заданную нелинейность. Тот факт, что используются две частотные составляющие, а не одна, делает эквивалентную линеаризацию по двухчастот-ному входному сигналу более точной, чем обычная линеаризация. При вычислении эквивалентных передаточных функций для двухчастотного входного сигнала принимаются во внимание амплитуды входного и выходного сигнала и сдвиг фазы по обеим составляющим. Всеми остальными составляющими пренебрегают.;

Вообще говоря, вычисление эквивалентной передаточной функции для двух входных сигналов даже для простйх однозначных нелинейностей - достаточно трудоемкая задача. Только простейшие нелинейности типа степенных функций и идеальное реле позволяют получить эквивалентные передаточные функции в замкнутой форме. Для случая других нелинейностей эквивалентные передаточные функции для двухчастотного входного сигнала можно определить с помощью цифровых вычислительных машин, используя численные методы.

Эквивалентную передаточную функцию для двухчастотного входного сигнала можно применить для исследования субгармонических колебаний (§ 7.2), для нахождения дополнительных гармоник автоколебаний (§ 7.3) и для анализа явления синхронизации (§ 7.3).

Если одна из частотных составляющих, которая должна быть проанализирована, является постоянной, то применение эквивалентной передаточной функции для двухчастотного входного сигнала становится намного проще. Это показано в § 7.1. Действительно, когда частота одной составляющей

* В системах управления с гидравлическими усилителями переменная составляющая уничтожает явление облитерации ( залипания плунжера гидравлического усилителя) и тем самым обеспечивает работоспособность системы {Прим. ред.).

значительно выше другой, то в качестве основной составляющей можно выбрать постоянную составляющую, что значительно упрощает расчеты. Используя этот факт, можно проанализировать работу целого класса систем, известных как колебательные сервомеханизмы (§ 7.5). Данный класс систем обнаруживает свойства адаптации, связанные с нечувствительностью частоты автоколебаний к изменениям параметров объекта.

Если частоты составляющих входного сигнала несоизмеримы или их амплитуды или частоты значительно отличаются, то эквивалентную передаточную функцию для двухчастотного входного сигнала для случая некоторых типовых нелинейностей можно определить, описав нелинейность в интегральной форме (§ 7.4). В остальных случаях следует прибегать к помощи вычислительных машин.

7.7. ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ

7.1. Объясните, почему обратная эквивалентная передаточная функция для двухчастотного сигнала ViaNs) для идеального реле, изображенная на рис. 7.8, б, представляет собой окружности для ft 3, и найдите амплитуду составляющей третьей гармоники в примере 7.3.

7.2. Проанализируйте решение уравнения Дуффинга (пример 7.2) при а-< 0. Возможно ли в системе

а) появление субгармонических колебаний;

б) явление синхронизации?

7.3. Рассмотрите автономную систему (Фиттс), показанную на рис. 6.5, состоящую из линейного объекта

1{р + 0,01) + (о,т Up + 0,01)2 +

и нелинейности f (е) ~ 10е [51]. Покажите, что:

а) для этой системы вьшолняется гипотеза Калмана, Докажите, что-применение метода . гармонической линеаризации исключает возможность автоколебаний;

б) используя эквивалентную передаточную функцию для двухчастотного входного сигнала, покажите, что в системе возникают автоколебания вида е = а sin (со/ -- Ф) -f- Р sin Зсо/. Найдите величины а, Р, со и Ф.

7.4. Определите эквивалентную передаточную функцию для двухчастотного входного сигнала, если нелинейность задана функцией

сигнал на входе имеет вид

е (/) = ai sin (со/ -f- Ф) -f- sin hat.

Найдите (а, ah, Ф) и Nh (cci, ah, Ф) Для /г = 2, 3, 4.

7.5. Рассмотрите, при каких условиях система, показанная на рис. 6.5, имеет предельный цикл, если пользоваться эквивалентной передаточной функцией для двухчастотного сигнала, а не обычной эквивалентной передаточной функцией.

7.6. В качестве примера, раскрывающего трудности, с которыми связано применение эквивалентной передаточной функции для двухчастотного входного сигнала, рассмотрите задачу определения амплитуды третьей гармоники автоколебаний, которые описываются уравнением Ван-дер-Поля

х + \0{х-\)х+ х=0.

7.7. Для системы, показанной на рис. 7.15, найдите постоянную составляющую, амплитуду и частоту колебаний для = О и = 8. Оцените величину третьей гармоники колебаний.

7.8. Проанализируйте систему из примера 7.1, если А = 2, В = 1 и G (р) = = 60/ [(р -f 1) (р + 2) (р -f- 3) ], построив кривые, подобные изображенным на рис. 7.3, а, б, в.

7.9. Докажите следующие утверждения относительно эквивалентной передаточной функции (7.20):

а) для заданных величин а и д, когда Ф изменяется от О до 2я, годограф -i}lNi) описывает окружность на плоскости комплексного переменного;

б) все эти окружности расположены внутри сектора, показанного на рис. 7.7.