в этой главе мы обсудим приемы анализа систем на фазовой плоскости Начав с примера, перейдем к анализу отдельных точек и целых зон равновесия. Затем рассмотрим фазовые траектории линейной системы и приступим к изучению предельных циклов в нелинейных системах, попутно остановившись на многообразии видов поведения нелинейных систем. В заключение изложим методы построения фазовых портретов.

4.1. НЕКОТОРЫЕ ПРИМЕРЫ ТРАЕКТОРИЙ НА ФАЗОВОЙ ПЛОСКОСТИ

Прежде всего рассмотрим одну линейную систему второго порядка, чтобы показать целесообразность ее анализа с помощью фазовой плоскости.

Пример 4.1. Рассмотрим задачу управления движением искусственного спутника Земли в плоскости тангажа. В процессе управления требуется непрерывно осуществлять Направление ориентацию антенны спутника на выбранные звездные на звездный ориентиры (рис. 4.1). Управление положением дости-ориеитир гается с помощью пары двигателей, работающих в релейном режиме, что позволяет создать максимальный управляющий момент величиной Т или иметь нулевое управление. Пусть звездный ориентир расположен под углом 9 к оси телескопа, тогда уравнение движения спутника под действием управляющего момента т от реактивных двигателей можно записать в виде

Антенна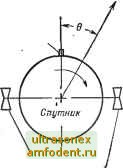

уе = т.

(4.1)

-Реактивные двигатели -

где J - момент инерции искусственного спутника Земли; т - управляющий момент, который может принимать значения -\-Ju, -Ju или 0.

Пусть и - -j- и .

(4.2)

Рис. 4.1. Схема управления положением искусственного спутника Земли в плоскости тангажа при его ориентации на звезду

Кх = 6; Ki (io) = Xio, Ха = 6; х, ((ф) = хо,

тогда уравнение (4.1) можно преобразовать к виду

Xi = Х2; Х2 = и. (4.3)

Структурная схема такой системы показана на рис. 4.. Рассмотрим, пользуясь рис. 4.2, следующие случаи. Случай 1:к=0. Уравнения (4.3) сводятся к системе Xi = х, Xg = О, рещение которой имеет вид

Х2 ~ -20 1 ~ -10 ~Ь 20

Траектории -этой системы на фазовой плоскости (фазовый портрет), зависящие от начальных условий Xjja и Хго, показаны на рис. 4.3, а.

Траектории являются прямыми линиями, параллельными оси х. Движение по траекториям, расположенным над осью х, происходит с течением времени в направлении роста координаты Xi, движение по траекториям Б нижней полуплоскости - в направлении убывания координаты Xi- На самой оси х движения не происходит, поскольку 2 = 1 = 0. Все это означает, что Б отсутствии управляющего момента искусственный спутник будет вращаться с постоянной угловой

Для рассматриваемого случая

Рис. 4.2. Структурная схема искусственного спутника Земли как объекту управления

скоростью, определяемой начальными условиями, условия равновесия выполняются, если х = Ха = О и, следовательно, ось Xi является зоной равновесных состояний.

Случай 2: и= +U. Интегрируя уравнения системы (4.3), получим

Xi= Xio+ 20*+ -ir X2=X20+Ut.-

где хщ и - начальные условия.

Поскольку траектории движения следует строить на плоскости в координатах и х, то необходимо исключить время. Это можно выполнить следующим образом. Запишем соотношение

dxi dt

dx dx и

при H = -f-t/;

инте рируя полученное дифференциальное уравнение, получим

= с для и = + и.

(4.4)

(4.5)

где с - постоянная интегрирования.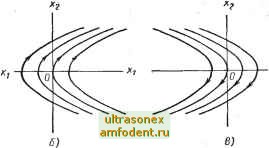

Рис. 4.3. Траектории движения спутника Земли в координатах

(Xl, ху.

о-при и - 0; 6 - при и = +U; в - при и = -U

Таким образом, траектории системы представляют параболы, изображенные на рис. 4.3, б. Нетрудно заметить, что все эти параболы имеют одинаковый вид.

Из рис. 4.3, б также видно, что есть лишь одна парабола, проходящая через начало координат. Если начальные условия таковы, что изображающая точка расположена ниже оси Xl на параболе, проходящей через начало координат, то, приложив момент +(/ при движении к началу координат и выключив реактивные двигатели при достижении начала координат, мы осуществим требуемую ориентацию телескопа, установленного на искусственном спутнике Земли, на звезду. При других начальных условиях, используя только положительный управляющий момент, этого добиться нельзя.

Следует также отметить, что в рассматриваемом случае при к = +1/ на фазовой плоскости не существует ни одного положения равновесия.

Случай 3:к = -U. Этот случай подобен случаю 2.

Заменяя в уравнениях (4.4) и (4.5) -\-U на -U, получим

dx и

Решение этого уравнения имеет вид

для и - -и.

(4.6)

. -f- Uxi = с при и = -U,

(4.7

где, как и раньше, с - постоянная интегрирования.

Фазовый портрет представляет семейство парабол, показанных на рис. 4.3, е. Лишь в том случае, когда в начальный момент времени изображающая точка расположена на кривой, проходящей через начало координат рис. 4.3, в, можно достичь начала координат, приложив единственное управление - (7. В этом случае также отсутствуют положения равновесия на всей фазовой плоскости.

Случай 4. Замкнув объект управления с помощью обратной связи и реле, мы получим простейшую систему автоматического управления (рис. 4.4). Здесь осуществлена связь

выходного сигнала (t) (угловое положение спутника 6 (f)) с управляющим сигналом и (О или, по существу, с реактивным моментом т (/) = с помощью реле

и (О = ~и sign Хх (О,

(4.8)

где sign X =

4-1, х>0; . -1, л:<0.

Выбирая требуемые сочетания траекторий на рис. 4.3, б и е с учетом управления (4.8), получим фазовый портрет системы с обратной связью, как показано на рис. 4.5. Каждая из фазовых траекторий является замкнутой и определяется начальными условиями. Таким обра-

-x,(t)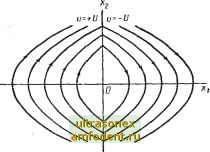

Рис. 4.4.Простейшая структурная схема системы управления искусственным спутником Земли

Рис. 4.5. Фазовый портрет для системы управления, изображенной на рис. 4.4

зом, J системе возникает и не прекращается движение в предельном цикле до тех пор, пока топливо не будет израсходовано полностью. При этом спутник соверщает незатухающие колебания относительно положения равновесия. Колебания в значительной степени присущи именно нелинейным системам, и поэтому при рассмотрении нелинейных систем их анализу уделяется большое внимание.

Случай 5. Введем в систему управления (рис. 4.4) идеальное дифференцирующее звено первого рода (p-f- а). Это сделано для того, чтобы в системе не возникали колебания.

Ноэффиииент наклона - с

u(t)

x,(t)

Рис. 4.6. Система управления искусственного спутника Земли с включенной идеальной фазоопережающей цепью р+а

Рис. 4.7. Типовые траектории движения искусственного спутника Земли (волнистой линией на участке В обозначено движение в скользящем режиме)

а координаты Xi и Xg монотонно приближались к началу координат. Тогда телескоп будегг непрерывно отслеживать положение звездного ориентира.

Допустим, что сигнал, прежде чем включить двигатель, подвергается фазоопережающей линейной коррекции. В этом случае в системе реализуется элемент предсказания. Для того чтобы оставаться в рамках систем второго порядка, рассмотрим идеальную фазоопережающую цепь вида р+а. Тогда система управления искусственного спутника Земли может быть представлена структурной схемой, показанной на рис. 4.6.

Для данной схемы управление принимает вид

и (t) = -С sign(Xi -I- axi) = -U sign (xg + ax).

(4.9)