Автоколебательная проверка дает хотя и грубую, но все-таки информацию, исходя из метода гармонической линеаризации. Предполагается, что такой подход будет более точен, если выполняется условие фильтра. Однако это условие не всегда выполняется, и поэтому на эквивалентные амплитудно-фазовые характеристики по первой гармонике могут оказывать влияние высшие гармоники входного сигнала. Проникновение в физическую сущность и проведение соответствующих замеров сигналов в процессе автоколебательной проверки может помочь выяснить влияние высших гармоник.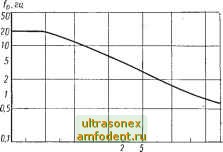

ЦИ Ц02 D.D5 0.1 0.2 0.5 1

W 20 50 W0 у

Рис. 6.29. Типовая зависимость у от и при создании контрольных автоколебаний (запас устойчиво-

сти по амплитуде Кс (у) = :

1. - реальная система; 2 - линейная система

Рис. 6.30. Зависимость частоты основной гармоники автоколебаний fo от у, полученная при проверке системы на автоколебания и определении времени переброса в системе

Автоколебательная проверка дает возможность определить запасы устойчивости по амплитуде, связанные со свойствами системы по отношеник> к гармоническому сигналу, но при этом остается открытым вопрос о других типах неустойчивых движений в системе. Таким образом, получаемые результаты эквивалентны использованию метода гармонической линеаризации. Однако автоколебательная проверка не позволяет выявить характер неустойчивости. Правда, в большинстве практических случаев в этом и нет необходимости.

6.8. СЛУЧАИ, КОГДА МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ НЕ ПРИМЕНИМ

Мы уже упоминали о том, что метод гармонической линеаризации, будучи приближенным, не всегда применим. Рассмотрим те случаи, когда этот метод не дает верного решения. Нетрудно показать, что для однозначных нелинейностей случаи, когда метод гармонической линеаризации справедлив встречаются столь же часто, как и случаи, когда выполняется гипотеза Айзермана. Если быть более конкретными, то легко показать (упражнение 6.15). что во всех случаях, когда гипотеза Айзермана не выполняется в силу существования предельного цикла, метод гармонической линеаризации также несправедлив. Так, например, последний метод не решает вопроса о существовании предельного цикла для системы, описываемой уравнением (5.87). Любая система, для которой доказано, что нарушается гипотеза Айзермана [42], [51] и [160], служит одновременно и контрпримером для метода гармонической линеаризации.

Поскольку метод гармонической линеаризации можно применять к анализу систем с двузначными нелинейностями, то ясно, что он справедлив для большего числа случаев, нежели гипотеза Айзермана. Несправедливость этой гипотезы и метода гармонической линеаризации связана с тем, что характеристика линейной части системы имеет значительные резонансные пики. Это и есть те самые случаи, о которых всегда предупреждают инженеров, призывая их быть осторожными при исрользовании метода гармонической линеаризации.

Можно дать физически разумное объяснение, почему в рассматриваемых случаях метод гармонической линеаризации несправедлив (см. упражнение 6.16). Это будет сделано в следующей главе при изучении метода эквивалентной линеаризации при двухчастотном входном сигнале.

□ 6.9. КРАТКОЕ СОДЕРЖАНИЕ

Метод гармонической линеаризации и связанные с ним различные приемы весьма удобны для анализа и синтеза широкого класса систем управления и, в частности, систем высокого порядка. Эти методы дают возможность выяснить существование и устойчивость колебаний, присущих предельному циклу, если нелинейная система находится в свободном состоянии. Методы являются приближенными и требуют, чтобы высшие гармоники, генерируемые нелинейностями, не оказывали существенного влияния на работу системы. В этом случае ими можно пренебречь и учитывать лишь первую гар-.монику предполагаемых колебаний в контуре. Затем, выписав необходимые условия автоколебаний, можно отыскать либо аналитически, либо графически амплитуду и частоту этих колебаний, если они существуют. Обычно такие методы применимы для систем с четко выделенной линейной и нелинейной частями (см. рис. 6.5). Когда вид нелинейности достаточно прост (например, однозначная кусочно-линейная характеристика или простая нелинейность с гистерезисом), то эквивалентная передаточная функция может быть определена из табл. 6.2, тогда линейные методы, связанные с использованием частотного годографа или логарифмических амплитудно-фазовых частотных характеристик, можно с успехом применить для определения условий автоколебаний.

Широкое использование метода гармонической линеаризации связано главным образом с тем, что метод позволяет анализировать сложные системы. Во-первых, можно определить условие скачкообразного резонанса в системах, показанных на рис. 6.5, при синусоидальном входном сигнале. Явление скачкообразного резонанса по фазе в замкнутой системе, включающей элемент с насыщением, было впервые объяснено Лозьером [128] (§ 6.5). Во-вторых, метод гармонической линеаризации позволяет оценить запасы устойчивости нелинейной системы как для малых, так и больших сигналов в системе, вводя понятие запас устойчивости по амплитуде в нелинейной системе. Такую характеристику можно найти для замкнутой нелинейной системы в свободном состоянии, если она состоит из одного или большего числа внутренних контуров. Этот подход позволяет также осуществить в контуре нелинейную коррекцию, как это подробно рассмотрено в § 6.6. Если запас устойчивости по амплитуде в нелинейной системе определяется так, как это обычно принято, то это чрезвычайно трудоемкий процесс. В § 6.7 дается удобный прием определения этой характеристики для систем высокого порядка. Такой подход был с успехом использован авторами на практике. Однако, несмотря на все сказанное, возможности метода гармонической линеаризации еще далеко не исчерпаны.

6.10. ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ

6.1. Рассмотрите систему тх-\- kx\x\ = 0:

а) получите общее решение в фазовой плоскости (отметим, что система консервативна);

б) используя метод гармонической линеаризации, определите возможность автоколебаний в системе; если они существуют, найдите их период и амплитуду;

в) сравните результаты пункта б) с точным решением, полученным при непосредственном интегрировании исходного уравнения.

6.2. Выведите эквивалентные передаточные функции для нелинейностей 6; 11 и 23 (см. табл. 6.2).

6.3. Как следует преобразовать систему, структурная схема которой содержит нелинейность с произвольным уровнем ограничения (см. рис. 6.5)?

kx, \х\а; ka, x> а; . -ka, X < -а,

чтобы можно было при выводе использовать результат для нелинейности с единичным уровнем ограничения, указанный в табл. 6.2.

6.4. Исследуйте систему с идеальным реле амплитуды f/ и с передаточной функцией линейной части (см. рис. 6.5)

G (р) = -

р(р + а).

а) определите существование и устойчивость в малом всех возможных положений равновесия;

б) исследуйте существование и устойчивость всех предельных циклов методом эквивалентной линеаризации;

в) определите положения равновесия и амплитуды и частоты предельных циклов для следующей последовательности параметров:

(7=2; В = 10 Усек; 6 = 25 Усек; а = 1 Усек;

г) для постоянного входного сигнала найдите среднее значение выхода в установившемся состоянии.

6.5. Рассмотрите линейную стационарную систему порядка п с парами различных чисто мнимых полюсов. Пусть числовые значения полюсов будут несоизмеримы, т. е., если полюсы

равны р = ±/pi, ±/р2, . ., то отношение при i ф k не является отношением целых

чисел. Изучите свободное движение системы в каждой точке фазовой плоскости. Является ли оно: устойчивым; орбитально устойчивым; периодическим; ограниченным?

6.6. Для системы из примера 6.3 найдите графически амплитуду и частоту автоколебаний, построив годограф амплитудно-фазовой характеристики линейной части системы и зависимость --(см. раздел 6.2), пользуясь уравнением (6.15).

6.7. Для структурной схемы системы, изображенной на рис. 6.5 с нелинейностью типа люфт (строка 22 в табл. 6.2) и для

П \ -40

а) используя метод гармонической линеаризации, определите Диапазон изменения коэффициента наклона k нелинейной характеристики, когда автоколебания ие существуют; аргументируйте сделанные предположения;

б) для значений k, при которых автоколебания существуют, постройте кривые зависи-

мости частоты соо и относительной амплитуды автоколебаний от величины k в дб;

в) объясните, что пр.оисходит, когда значения k лежат ниже или выше той области, где существуют автоколебания;

г) определите состояния равновесия и их устойчивость для всех трех диапазонов изменения коэффициента k (указание: для анализа эквивалентной передаточной функции использовать метод корневого годографа).

6.8. Метод гармонической линеаризации основывается на предположении о том, что высшие гармоники на выходе нелинейного элемента затем фильтруются линейной частью кон-