Из примера 10.6 видно, что линейная часть, описываемая соотношениями (10.37), будет устойчива при замыкании отрицательной обратной связью с коэффициентом О <С Л < 30. К тому же линейная часть устойчива и без охвата обратной связью. Следовательно, условия теоремы 10.5 выполняются для любого нелинейного элемента, расположенного в полуоткрытом секторе (к/е) £ [О, К], и неравенство Попова имеет вид

Re о; (/ш) > -L + 9 Im о; (/ш).

Рис. 10.12. Модифицированный частотный годограф для передаточной функции Ga (s) =- . /-j-rT- примера 10.8

s (s i) (s -j- о)

Модифицированная частотная характеристика G* (/ш) для а = 12 изображена на рис. 10.12. Через точку с координатой*G*(/cu) = - можно провести прямую Попова с на-

клоном -г. Последнее означает, что условия теоремы 10.5 выполняются при ? = 1,2, если

характеристика стационарной однозначной нелинейности а = /с ifi) расположена в секторе {uje) (0,30) 1).

Для общего случая нелинейной характеристики или для характеристики с пассивным гистерезисом прямая Попова соответствует условию ? == О и представляет вертикальную линию. Определяя в этом случае сектор Попова, получим (Ыд/е) £ (0; 4,17), который существенно меньше сектора (Ыд/е) £ (0; 30) для стационарной однозначной нелинейности.

Мы проанализировали систему, которая была получена из выражения (10.32) сдвигом полюсов [преобразование (10.29)]; поэтому следует распространить полученные результаты на исходную систему. Согласно выражению (10.29) при а = 12 получим секторы Попова [ule) 6 (12; 42) для однозначной (или с активным гистерезисом) стационарной нелинейности и (ule) Е. (12; 16,71) для общего вида нелинейности.

) Условия теоремы выполняются и для нелинейности с активным гистерезисом.

в примере 10.7 мы пытались воспользоваться теоремой 10.5 для анализа исходной (непреобразованной) системы, однако при этом не существовало сектора Попова при произвольном виде нелинейной характеристики. Это, как уже указывалось, обусловлено тем, что теорема 10.5 представляет лишь частный, -достаточный вариант теоремы 10.4. Если бы мы хотели получить

imgiju) - 0.0в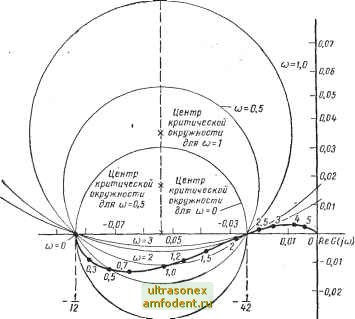

0.03

Рис. 10.13. Частотный годограф G для передаточной функции G (s) = --is / очг 1/14 к примерам 10.6, 10.7 и 10.9

(s-l)(s+3)(s+4)

частотный критерий для анализа исходной системы, не пользуясь преобразованием, связанным со сдвигом полюсов, то нам следовало бы воспользоваться теоремой 10.4.

Пример 10.9. Для системы из примеров 10.6 и 10.7 определить сектор Попова для стационарной однозначной нелинейности и = f (е), воспользовавшись теоремой 10.4.

Прежде всего заметим, что линейный элемент, охваченный отрицательной обратной связью с коэффициентом 12 <; а <; 42, устойчив. Используя теорему (10.4), можно определить значение q, а именно: q = 1,2, которое позволяет провести критические окружности, проходя-ш,ие через точки -1/12 и -1/42 и такие, что при каждом значении ш соответствующее значение G (ja) определяет точку на или вне соответствующей критической окружности (рис. 10.13). Сектор Попова в этом случае равен (ы/е) £ (12; 42).

Заметим, что указанная процедура анализа достаточно сложна. Самое трудное - отыскать нужное значение q, для которого выпелняется круговой критерий. Этот поиск можно вести методом последовательных приближений. В данном случае, исходя из предьщущих рассуждений, можно было ожидать, что 9= 1,2 является подходящим значением. Рис. 10.13 подтверждает это. Вообще говоря, отыскание приемлемого значения q методом последовательных приближений - достаточно трудоемкое занятие. Сравнивая данный пример с предыдущим, замечаем, что целесообразно сначала преобразовать исходную систему в систему с сектором Попова (uJe) [О, b - а], а затем поступить так, как в примере 10.8.

Итак, два подхода дали одни и те же результаты, но этого может и не быть, если рассматривать нелинейности более общего вида; и тогда прямой

метод, не связанный со сдвигом полюсов исходной системы, а основанный на теореме 10.4, будет давать более общие результаты, чел1 непрямой метод примера 10.8. Покажем это на примере.

ImG(jU)

16.71

, Рис. 10.14. Частотный годограф для исходной передаточной функции 0()= (, i)(,+3)(s+4) P P (10.6)-(Ш.10)

Пример 10.10. Используя теорему 10.4, определим для исходной системы (10.32) сектор Попова, имея нелинейную характеристику общего вида ы = [е (Q, t\. Поскольку рассматривается нелинейность общего вида, то следует положить = 0. По теореме 10.4 можно найти такие секторы Попова ( /e) £ (с, 6), что для каждого из них частотный годограф G (/ю) расположен либо на окружности *, симметричной относительно действительной оси и проходящей через точки -1/а и -1/6, либо вне ее. В данном случае нетрудно определить (рис. 10.14), что секторы (ы/е) £ (12; 16,71); (ы/е) G (14; 20) и (ы/е) £ (23; 31) являются секторами Попова. В то же время видно, что размер сектора Попова или разность между верхней границей Ъ и нижней о зависит от размера критической окружности, который, в свою очередь, определяется значением а. Указанная зависимость получена из рис. 10.14 и представлена на рис. 10.15.

Непрямой метод примера 10.8 дал возможность отыскать единственный сектор Попова (ы/е) £ (12; 16,71). При использовании кругового критерия (теорема 10.4) оказалось возможным отыскать цеЛ5Т0 область секторов, в которую входит и сектор, найденный в примере 10.8. Из рис. 10.15 следует, что при нижней границе а- 20 определяется сектор Попова максимального размера, а именно: (ы/е) £ (20; 28,5). Отметим, хотя этого и следовало ожидать, что и этот сектор Попова лежит внутри угла Гурвица, т. е. угла, внутри которого всякая линейная стационарная система с обратной связью и - he устойчива.

Рассмотренные примеры, начиная с 10.6 и кончая 10.10, показывают, что не существует универсального способа решения любой задачи. Иногда целесообразнее применять основную теорему 10.1 к преобразованной в результате сдвига полюсов системе; в других случаях целесообразнее применить теорему 10.4 или 10.5 к исходной системе. Из этих же примеров следует, что круговой критерий, изложенный в теореме 10.4, в большей степени приемлем для случая = О, т. е. для нелинейных характеристик общего вида. Подробнее этот вопрос освещается ниже.

* Если рассматривается открытый сектор Попова (и/е) (о, Щ, то частотный годограф G (/со) может касаться критической окружности.

Рис. 10.15. Величина сектора Попова (fc-а) в зависимости от нижней границы а для системы из примера 10.10