циклов необходимо ввести понятие орбитальной асимптотической устойчивости. Анализ предельных циклов в автономных системах второго порядка можно выполнить с большой наглядностью.

Пример 4.4. Пусть система описывается уравнениями

=y-x(x + y-iy, --.х-у(х + у-

(4.32)

В такой системе сущестйует устойчивый предельный цикл на окружности единичного радиуса. Чтобы убедиться в том, перейдем к полярным координатам

= г(г2-1);

Если г<3 1, то силы, действующие на систему, будут вызывать рост г, если / > 1, то г будет уменьшаться; когда г= 1, то никаких сил, вызывающих изменение г, нет, и движение по кривой г = 1, О = Go + t может сохраняться неограниченно долго.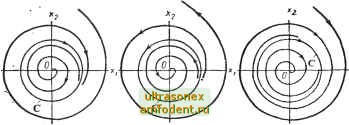

Рис. 4.18. Виды предельных циклов.в нелинейных системах:

о- устойчивый предельный цикл С; \6-неустойчивый предельный цикл G; в --полуустойчивый предельный цикл С

Аналогично можно показать, что в системе dx

= у + х(х + у-\\.

= -х-\-у(х-\-у-\).

= -х-у (х + у-1)

(4.33)

(4.34)

существует неустойчивый предельный цикл. Можно показать, что в системе

у-Х{Х+У-\)

существует полуустойчивый предельный цикл.

Наряду с существованием предельных циклов в нелинейной системе может наблюдаться сразу несколько видов поведения. Такое явление либо имеет место в системе с несколькими положениями равновесия, либо разный тип траекторий наблюдается в нескольких областях фазовой плоскости в окрестности равновесных состояний. В последнем случае граничная траектория, отделяющая области с различными видами движения, называется сепаратрисой.

В этом случае имеем dt

= г(г2-1); - = -1 {Прим. ред.)

** Здесь имеем

r{r-l)H =-1 (Прим. ред.).

Следующий нетривиальный пример иллюстрирует, как проявляется на практике многообразие траекторий одной и той же нелинейной системы.

Пример 4.5 188). Рассмотрим систему, состоящую из последовательного соединения электродвигателя с генератором, показанную на рис. 4.19. Если такая система рассчитана правильно, то скорость электродвигателя оказывается не зависящей от нагрузки. Для данной схемы примем следующие допущения:

1. Магнитные цепи обеих машин имеют вид показанный на рис. 4.20.

2. Оба устройства насыщаются при одном уровне тока, но не обязательно при одинаковых уровнях магнитного потока.

3. Генератор вращается с постоянной скоростью

Постоянная скорость Вращения генератора

Рис. 4.19. Система, состоящая из последовательно соединенных электродвигателя и генератора

Рис. 4.20. Кривая намагничивания для электродвигателя и генератора

При этом уравнения движения системы будут

fi(f)i{t)=d + bv {t)-\-Tj Ф (О = [i (0].

(4.35)

где i (t) - ток в цепи; и (Q - скорость вращения электродвигателя; (Q = [ (О J - магнитный поток

Зависимость [t (0] от тока t (t) показана на рис. 4.20.

Оставшиеся величины являются параметрами этой системы- В частности d характеризует постоянный момент нагрузки на электродвигателе; Ъ определяет момент нагрузки на электродвигателе, пропорциональный угловой скорости его вращения.

Уравнения (4.35) определяют существенно нелинейную систему второго порядка, и ее поведение при различных комбинациях параметров достаточно сложно [88]. Сейчас нас интересуют лишь некоторые специальные случаи движения. Допустим, что параметры системы имеют следующие значения: = 1; Чтаах = 1,5; М = \ \ а - 0,2; Г/ = 50 тек, Т - 30 жек; Те = 60 мсек; Ь = 5; d = 0. Тогда положения равновесия определяются из условий

0,2t = (1 - и) Ч; = 5u.

(4.36)

Если решать систему уравнений (4.36), используя кривую намагничивания со значением Чшах = 1,5, то мы получим три положения равновесия. Первое в начале координат i = 0; i) = 0. Второе и третье расположено в точках i = ±2,31; v = 0,692. Фазовый портрет, полученный моделированием на аналоговой вычислительной машине, показан на рис. 4.21. Видно, что первое положение равновесия в начале координат напоминает седловую точку, в то время как второе и третье похожи на устойчивые фокусы. Весьма интересный случай будет иметь место, если положить 6 = О и d= 1, сохранив значения остальных параметров прежними *.

Для этого случая Чпих = 1 (Прим. ред.).

в этом случае состояние равновесия из начала координат уходит в бесконечность, в точку с координатами i = О, v = - оо, в то время как второе и третье равновесные состояния располагаются в точках i = ±1,00; v = 0,8. Фазовый портрет системы показан на рис. 4.22. Здесь мы сталкиваемся с необычным явлением; в непосредственной близости от двух последних положений равновесия расположены области, заполненные замкнутыми кривыми. Однако вне этих областей все траектории представляют спирали, направленные к двум замкнутым кривым, подобным предельному циклу. Эти замкнутые кривые и определяют на фазовой плоскости сепаратрисы, которые выделяют области с разными видами траекторий.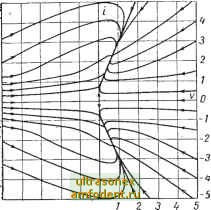

-5 -й -3 -2 -7 О

Рис. 4.21. Фазовый портрет системы (рис. 4.19) в координатах (г, v) при Е=1; W= 1.5; Л1= 1,0; а = 0,2; Tj = 50 мсек; Т = 30 мсек; Те = = 60 мсек; Ь = 5; d = О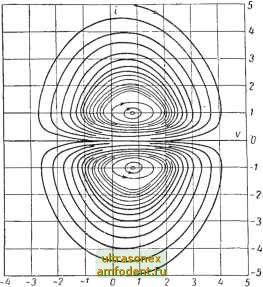

Рис. 4.22. Фазовый портрет системы (рис. 4.10) при tjiniax - 1.0; 6 = О и d = 1; остальные параметры сохраняются прежними (см. рис. 4.21)

4.5. ФАЗОВЫЕ ТРАЕКТОРИИ КОНСЕРВАТИВНЫХ СИСТЕМ

Консервативными системами называются системы, динамика которых описывается дифференциальным уравнением вида х -j- f (х) = О, в котором отсутствует член с координатой х, определяющий меру демпфирования или потери энергии в системе. Следовательно, в консервативных системах запас энергии остается неизменным. Чтобы убедиться в этом, запишем уравнения системы в виде Xi = х; х, = -f (Xj), или иначе

dX2 f(Xy)

Уравнение (4.37) можно проинтегрировать и получить

-t- J fix)dx = E,

(4.37)

(4.38)

E - постоянная интегрирования.

Первый член уравнения (4.38) определяет кинетическую энергию системы, второй - потенциальную энергию. Координата х определяет положение равновесия, относительно которого измеряется потенциальная энергия, а значение постоянной Е - полную энергию системы. Понятно, что последняя величина зависит от начальных условий. Для каждого заданного значения Е уравнение (4.38) определяет траекторию системы.