где использовано соотношение

для всех п.

В пределе можем записать

8u{t)

(8.75)

где [lo (i) - единичный импульс при t = 0. Уравнение (8.75) вместе с соотношениями для переменных 8и (/), ду (t) и бг (/) описывает импульсную систему управления, изображенную на рис. 8.15.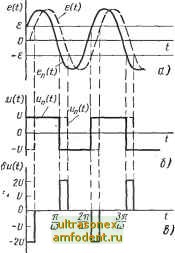

eft)

e(t)

e(t)

-£

ejt)

e(t)

Рис. 8.13. Виды сигналов е (t), et), и (f), и (t) и ёи (t) при действии малых возмущений на релейные системы управлений

Рис. 8.14. Соотношения между ёе (-1 и шириной пульсации

а - при перемючении реле с (-) на (+); б-при переключении реле

с {+) на (-)

Докажем теорему.

Теорема 8.2. Для системы управления, включающей реле без зоны нечувствительности (см. рис. 8.1),

устойчивость автоколебаний (входной сигнал r(t) = 0) или внутренних колебаний при периодическом входном сигнале {t) равносильна устойчивости линейной дискретной системы (рис. 8.15).

Отметим, что период прерывания импульсной системы (рис. 8.15) равен

т - = Тогда обратное модифицированное 2-преобразование с опережением равно

(8.76)

Для m = О - функция S (г, т) переходит в функцию (г), определяемую выражением (8.62).

На основании теорем 8.2 и II.4 приложения II сформулируем следующую теорему.

Теорема 8.3. В системах управления (см. рис. 8.1) с реле без зоны нечувствительности при условии, что

1) линейный элемент описывается обыкновенным дифференциальным уравнением с постоянными коэффициентами и является полностью управляемым и наблюдаемым;

2) для любых т функция (2, т) имеет те же полюсы, что и функция (2, 0) = (2);

3) все нули функции

1+ fix S{z) = 0 . (8.77)

лежат в области 2 < 1 ( z> 1), автоколебания или вынужденные колебания асимптотически устойчивы (неустойчивы).

ffr(t) few j ffg(t)

Линеаризованное реле I при палых кследательных I возпущениях

С(Р)

Sy(t)

Рис. 8.15. Структурная схема дискретной системы, эквивалентная релейной системе управления, показанной на рис. 8.1

Заметим, что условия 1) и 2) в формулировке теоремы 8.3 удовлетворяются в большинстве практических задач. Если все кор ни уравнения (8.77) лежат внутри круга \z\ < 1, за исключением одного или более корней при I z = 1, то так же, как и при анализе на основе первого метода Ляпунова, здесь требуются дополнительные исследования.

Раз допускается, что g- (0) = О, то можно к исследованиям привлекать критерий устойчивости, основанный на использовании функции Цыпкина J (со). Из выражения (8.65) имеем

(8.78)

G*(/co) = --ReJ(co).

Рассмотрим теперь случай, когда все полюсы передаточной функции G (s) расположены в области Re s <; О, за исключением, быть может, простого полюса при 5 = 0. Для импульсной системы управления, изображенной на рис. 8.15, амплитудно-фазовый критерий устойчивости требует выполнения условия

G*(/co)>-1. (8.79)

Это означает, что

Rey(co)>-1

Re/(co)>-

(8.80)

Условие (8.80) можно использовать для определения устойчивости вынужденных колебаний, когда они являются двухчастотными; например, в случае, показанном на рис. 8.12, б, где

-Ф)+ /( )}, (8.81)

(8.82)

Рис. 8.16. Годограф / (со) и линия - е. В точках и cOg наблюдаются устойчивые колебания, а в точке со 2 - неустойчивые

со \ со / со

поэтому условие (8.80) превращается в

Re / (соо) > - I Re [i? (я - Ф) + У (соо) j

А условие устойчивости удовлетворяется только тогда, когда

Re Ш (я - Ф) + / (соо) ] < Re7 (соо).

Таким образом, для случая, показанного на рис. 8.12, б, вынужденные колебания при Ф устойчивые, а при неустойчивые. Вообще колебания, определяемые пересечением кривой R (я-Ф) с линией - е, лежащей влево от точки J (соо), всегда будут устойчивыми. Если же эта точка пересечения

лежит вправо от точки J (cdq), то колебания будут неустойчивыми.

Сделаем общее заключение о свойствах вынужденных колебаний в системе управления с реле без зоны нечувствительности по методу Цыпкина.

1) Условия существования вынужденных колебаний:

Re [/?(я-Ф) + У(соо)] <0; Im [R (я - Ф) + У (соо)] = -е. .

2) Условие устойчивости:

Re [R{n-0) + J (соо) ] < Re/ (соо).

3) Условие неустойчивости:

Im [i? (я - Ф) + J (соо) ] > Re У (соо).

К сожалению, вышеприведенные зависимости не позволяют судить юб устойчивости автоколебаний, когда R (п-Ф) = О, и условие (8.82) вырождается.

Таким образом, случай автоколебаний требует дополнительного анализа в окрестности точки z = -1 единичного круга для характеристического уравнения (8.77). В этом случае имеем следующую теорему.

Теорема 8.4. Рассмотрим релейную систему (см. рис. 8.1) при г (/) = О с реле без зоны нечувствительности, полностью управляемую и наблюдаемую с линейным объектом, имеющим передаточную функцию G (s) с полюсами Re S <: О, за исключением, быть может, простого полюса s = 0. Если

ам ;>0 в точке, где У (со) пересекает линию Im У (со) = -е, то автоколебания не только устойчивы, но и обладают свойством орбитальной асимптотической устойчивости.

Доказательство этой теоремы приведено в гл. 11.

Для случая, показанного на рис. 8.16, автоколебания при со и сод устойчивы, а при cog неустойчивы.

Используя метод Цыпкина, нетрудно определить необходимые условия существования субгармонических колебаний *.

* Заинтересованный читатель может ознакомиться с этими результатами в работах 1173] и [60].