Гармоники, отличные от третьей, могут быть найдены таким же образом при условии, что известна соответствующая эквивалентная передаточная функция для двухчастотного входного сигнала.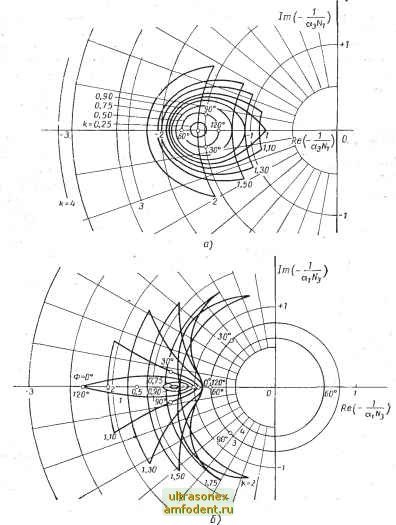

Рис. 7.8. Нормированные отрицательные обратные эквивалентные передаточные функции для двух сигналов идеального реле с единичным выходным сигналом, где а. и д - амплитуды

первой и третьей гармоник входного сигнала: а - график основной эквивалентной передаточной функции (а аУ, б - график эквивалентной; передаточной функции по третьей гармонике ( 1, о;з) при различных соотношениях k = --

2. Определение условий синхронизации

Явление синхронизации относится к очень своеобразному виду нелинейных колебаний. Оно возникает в тех случаях, когда система, в которой установились автоколебания с периодом Т, подвергается периодическому воздействию с периодом Tz =h (обычно < Т. Когда входной сигнал, имеет малую амплитуду, выходной сигнал системы содержит обе частотные

составляющие ©1 = и сй2 = риих гармоники. Если и не про-

порциональны, то выходной сигнал не будет периодическим. С увеличением амплитуды входного сигнала может наступить такой момент, когда выходной сигнал станет периодической функцией с периодом Т-

Другими словами, выходной сигнал будет синхронизирован с входным *. Таким образом, когда имеет место явление синхронизации, в системе не только прекращаются автоколебания с частотой соi, но и возникают колебания с частотой или кратной ей, и, следовательно, синхронизация или вынужденные колебания наиболее вероятны в том случае, когда сй близко

к со 2 или кратно cu2.

Пусть в системе возникли автоколебания с периодом Ti, затем на ее вход подали

сигнал R sinf-jT-W ; области синхронизации при этом определяются отношением TJT в зависимости от R. Эти области на рис. 7.9 заштрихованы. Отсюда видно, что при возникновении явления синхронизации период автоколебаний уменьшается. Покажем, как можно проанализировать вынужденные колебания или явление синхронизации, используя понятие эквивалентной передаточной функции для двухчастотного входного сигнала.

Системе, приведенной на рис. 6.5, прежде всего должны быть свойственны автоколе-

бания. Это означает, что существует частота сй при которой вы-

полняется следующее условие:

N (е) G Owi) = -1,

Рис. 7.9. Зоны синхронизации в типовой автоколебательной системе

при нескольких отношениях-

где N (ё) - обычная эквивалентная передаточная функция.

t + е

необходимо потре-

Теперь для входного сигнала R sin

бовать, чтобы ЗТг < Т, если нам нужно исследовать синхронизацию с периодом, близким к STg. Для сигнала на входе нелинейности в виде

е(0 - aisin [() i?+ф] + аз [sin (?) /

можно сразу же написать следующие два уравнения, пользуясь понятием эквивалентной передаточной функции для двухчастотного входного сигнала:

( 1, ссз. Ф) 3 (/ = (cos е -f / Sin G) - 1.

(7.24а) (7.246)

* Следует отметить, что явление синхронизации широко используется для получения телевизионного изображения.

Заметим, что решение уравнений (7.22) для определения третьей гармоники й уравнений (7.24) для определения условий вынужденных колебаний может оказаться очень трудным. При этом, возможно, придется прибегать к численным методам решения, используя цифровые вычислительные машины.

Для упрощения вычислений могут быть использованы следующие положения. Рассмотрим эквивалентную передаточную функцию для двухчастотного входного сигнала

е {t) = sin (<о -f 6) + а;г sin hat,

где h - целоечисло.

Если h достаточно велико, т. е. частоты далеки друг от друга, то можно считать, что значения фазы 6 становятся малыми, а эквивалентные передаточные функции Л/i и Nh принимают действительные значения. Для наших целей составляющую более низкой частоты можно аппроксимировать постоянным сигналом. Это позволяет использовать методы изложенные в § 7.1.

Если отношение амплитуд aja достаточно велико, то функции Л/i и Nh вновь можно считать действительными и использовать те же приближения.

7.4. ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ДЛЯ ДВУХЧАСТОТНОГО ВХОДНОГО СИГНАЛА НА ОСНОВЕ ПРЕДСТАВЛЕНИЯ ОДНОЗНАЧНЫХ НЕЛИНЕЙНОСТЕЙ В ИНТЕГРАЛЬНОЙ ФОРМЕ

Определить эквивалентную передаточную функцию для двухчастотного входного сигнала - это значит найти составляющие выходного сигнала нелинейного элемента, когда входной сигнал состоит из двух синусоидальных составляющих. Требуется найти составляющие выхода только при значениях частот входного сигнала и тем не менее для большинства нелинейностей это сделать достаточно трудно.

Полезный подход, пригодный для анализа однозначных нелинейностей, когда частоты входного сигнала coi и cog несоизмеримы * либо когда амплитуда или частота одной составляющей значительно больше, чем другой, заключается в представлении соотношения между входным и выходным сигналами в интегральной форме. Эта форма записи, кажущаяся на первый взгляд довольно громоздкой, во многих случаях после ряда преобразований может быть сведена к известным функциям, таким как гипергеометрические функции или эллиптические интегралы. Этот подход широко использовался Беннетом, Райсом и другими авторами **.

Прежде всего рассмотрим интеграл вида . . .

, е>0;

(7.25)

* Это имеет место, когда отношение не является рациональным числом. ** См. работу [81 ], в которой изложен этот метод более детально.