Другая крайность заключается в рассмотрении системы с коэффициентом усиления вместо нелинейного элемента. Из частотного критерия устойчивости следует, что для устойчивости замкнутой системы коэффициент усиления должен быть меньше, чем коэффициент, соответствующий пересечению годьграфа G Оо) с отрицательной полуосью действительной оси. На рис. 10.3а эта точка обозначена {-1К). Следовательно, максимальный коэффициент усиления должен быть меньше К (рис. 10.36). Та часть плоскости переменных {и, е), в которой может располагаться нелинейная характеристика и = [е (0. называется сектором Попова; допустимая область расположения линейных управлений вида и = he определяет угол Гурвица.

ImG(jcj)

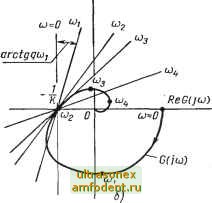Рис. 10.4: a) Иллюстрации условий устойчивости (10.19) и (10.20); б) Различное расположение прямой Попова на плоскости О (/со) при 9 < О

Поскольку стационарное линейное управление и = he удовлетворяет условию (и/е) € 10, К] для О /I /С и для линейных систем угол Гурвица определяет наибольшую область, в которой система устойчива, то ясно, что этот угол будет всегда больше или равен сектору Попова.

Перейдем к анализу общего случая, когда д ф 0. Выбирая подходящее значение д, мы можем расширить сектор, в котором должна располагаться характеристика нелинейного элемента. Однако при этом накладываются ограничения на сам вид нелинейности. Например, в силу условий теоремы 10.1, если q может принимать любое действительное значение, то нелинейная характеристика должна быть обязательно стационарной и однозначной.

Условие (10.19) можно переписать в следующем виде:

ReG(/o))> --1-4-0)9 ImG (/со); (10.20)

оно означает, что для любой частоты о годограф G (/ю) должен располагаться правее прямой, определяемой уравнением

Re G (; ) = --f 91ш G (/ ).

Эта прямая называется прямой Попова и показана на рис. 10.4а. Наклон прямой зависит от произведения 9 (рис. 10.46). Значение д необходимо выбрать таким, чтобы для любой частоты ю кривая G (jo) располагалась правее прямой Попова, соответствующей этой частоте. Для того чтобы упростить выбор q, воспользуемся следующим преобразованием [1].

Для этого определим модифицированную частотную характеристику линейной части с передаточной функцией G (s) следующим образом:

G* (/со) = Re G (/со) + /о Im G (/о),

другими словами.

Re G* (/(о) = Re G (/ю); Im G* (/со) = ю Im G (/о).

(10.21)

Годограф G* (/со) нетрудно построить, умножив мнимую часть G (/&)) на величину со. С учетом выражения (10.21) условие (10.20) можно записать в виде

Re G* (/со) > -L + 9 Im Q* (/со). (10.22)

arctgq

lrnC*(jiJ)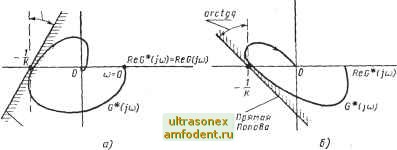

Прямая Попова

Рис. 10.5: а) Прямая Попова на плоскости О* (/со) для 9>0, приемлемая для однозначных нелинейностей и нелинейностей с гистерезисом; б) Прямая Попова для 9 < О, пригодная для систем с однозначной нелинейностью и пассивным гистерезисом

Последнее означает, что прямая Попова на плоскости G* (/со) определяется уравнением

Re G* (/(О) + 9 Im G* (/со)

и не зависит от частоты. Это положение иллюстрируется с помощью рис. 10.5а, б, рассматривая которые, можно сделать интересный вывод. Допустим, что нам удалось провести касательную к годографу G * (/со) в точке его пересечения с отрицательной частью действительной оси, когда весь годограф расположен правее этой прямой. Пусть эта точка имеет абсциссу (- C). Тогда К не только определяет максимальный возможный коэффициент усиления линейной системы с / (е) = he, но и определяет наибольшее возможное отношение / (е)/е. Для такой системы выполняются гипотеза Айзермана и условия существования абсолютно асимптотически устойчивых управляющего и выходного сигналов. Следовательно, если система (10.1) линейна, стационарна и w (f) = he {() и для нее существует асимптотически устойчивое управление и асимптотически устойчивый выходной сигнал для всех О Я /С, то система с произвольной стационарной однозначной нелинейной характеристикой и {{) =f {e{t)) также характеризуется асимптотически устойчивым управлением и асимптотически устойчивым

Это следует из частного критерия устойчивости.

О гипотезе Айзермана говорилось в гл. 5 в связи с изучением абсолютной асимптотической устойчивости.

выходным сигналом, поскольку f{0)=0 и Of {е)1еК- Отметим, что выполнение гипотезы Айзермана совместно с условием существования абсолютно асимптотически устойчивых сигналов управления и выхода означает.что сектор Попова и угол Гурвица совпадают.

Как правило, удается провести касательную такого вида. Таким образом, гипотеза Айзермана, будучи несправед-

u(t)

C(p)=

(p*2}(p-H.5)

Рис. 10.6. Пример, для которого сектор Попова меньше, чем угол Гурвица. Гипотеза Айзермана при этом не выполняется

Рис. 10.7. Нелинейная система с запаздыванием к примеру 10.4

лива для всех случаев, охватывает значительный класс систем, используемых на практике. Этот вывод согласуется с нашими замечаниями к гл. 5.

На рис. 10.6 показан случай, когда гипотеза Айзермана не выполняется. Тогда Ki > К, и, следовательно, угол Гурвица больше, чем сектор Попова. Заметим, что сектор Попова выделяет область, в которой выполняются достаточные, но не необходимые условия существования абсолютно асимптотически устойчивых управляющего и выходного сигналов. Поэтому, если К <if (е)/е < < Ki, то может оказаться, что в нелинейной системе сигнала управления и выходной сигнал являются абсолютно асимптотически устойчивыми. Таким образом, если характеристика f (е) располагается вне сектора Попова, то никаких суждений об асимптотическом поведении сигналов в системе сделать нельзя.

Пример 10.4. Для системы второго порядка с запаздыванием, показанной на рис. 10.7, определить максимально возможный коэффициент К, при котором имеется абсолютно асимптотически устойчивый выходной сигнал для (м/е) [О, /С].

Для линейного элемента заданы следующая реакция на начальные условия ео (О и импульсная переходная функция!

ео (t) = eie-i + е--;

g (О = (-1) - (10.23)

2е-2<-1)] ,( 1).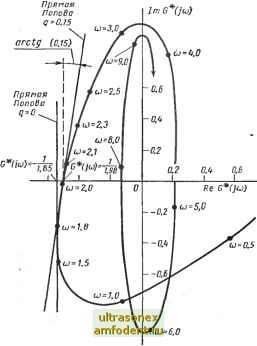

Рис. 10.8. Годограф G* (/со) = Re G (/со -f -f- /со Im G (/со) для линейного элемента системы, изображенной на рис. 10.7

где и 20 определяют начальные условия, а [х ] (t) - единичная ступенчатая функция. Заметим, что здесь линейный элемент устойчив. Годограф G* (/со) показан на рис. 10.8.