Как видно из рис. 6.5, к стандартному виду приводятся все одноконтурные системы управления. Многоконтурные системы управления со стационарной частью и выделенным нелинейным элементом можно также привести с помощью известных преобразований к-одноконтурной системе вида рис. 6.5 *.

Из примера предыдущего параграфа следует, что для рассматриваемого метода характерно:

1) предположение о существовании в точке е колебаний некоторой частоты;

2) определение условий, при к-оторых эти колебания существуют. Последнее допущение связано с тем, что не учитывается влияние всех

гармоник, которые возникают на выходе нелинейности. Сохраняются лишь характеристики нелинейности, связанные с передачей амплитуды и фазы основной частоты. i

Все сказанное выше равносильно тому, что мы заменяем нелинейный элемент Э, предполагаемый стационарным, другим нелинейным стационарным элементом Э, обладающим

Рис. 6.5. Структурная схема одноконтурной автономной нелинейной системы управления S

свойством передавать входной сигнал

е (f) =е sin ©/первой гармоники точно так же, как и элемент 3, но при этом какой бы ни была частота входного сигнала, на выходе Ш высшие гармоники отсутствуют. Заменив нелинейность Ш нелинейностью W, , можно приступить к точному анализу системы S, определяя условия, при которых предполагаемые колебания

е (f) = е sin ©if . могут существовать.

Заметим, что при любой амплитуде е и частоте © входного сигнала е (t) нелинейность Ш полностью определяется эквивалентной передаточной

функцией N {е, (а) = \ N (е, ©) е, где, как обычно, действительное число

I N (е, ©) I определяет усиление (ослабление) амплитуды е при прохождении

через нелинейность W, а величина Ф == arctg

Im N (е, w)

определяет фазо-

Re N (е, а)

вый сдвиг входной синусоиды при прохождении через нелинейность Ш.

Таким образом, если входной сигнал равен е (t) == е sin at, то выходной сигнал нелинейности W есть

u{t)=e\N(e, ©)18Ш(ю/ + Ф). (6.12)

Для того чтобы определить условие, при котором в системе S могут существовать колебания е (t) = е sin ©i, следует определить значения величин е и со, при которых эквивалентное усиление разомкнутой системы S становится равным -1. Это условие заключается в том, что

N (е, ©) G (/©) = - 1, (6.13) **

где G (/©) - частотная характеристика линейной части G (р).

* Подробнее см. Техническая кибернетика. Теория автоматического регулирования. Книга 3, часть 1, под ред. В. В. Солодовникова. Машиностроение , М., 1969 {Прим. ред.).

** В отечественной литературе соотношение (6.13) называется условием Гольдфарба {Прим. ред.).

Im[N(e,aj)G(jcj)]

Отметим, что по отношению к нелинейности 5 не имеет смысла говорить об усилении и фазовом сдвиге при синусоидальном входе. Однако по отношению к нелинейности W это становится верным. Кроме того, поскольку N (е, со) для нелинейности Ш можно вычислить, условие (6.13) проверяется различными способами. В частности, можно воспользоваться хорошо известными линейными методами.

1. Фиксируя амплитуду е, можно построить годограф передаточной функции разомкнутой системы, приняв в качестве параметра частоту со.

Построить семейство таких годографов для различных значений е. Значения амплитуды е и частоты со, при которых кривая проходит через точку -1; /О, определяют амплитуду и частоту автоколебаний в точке е (рис. 6.6). Отметим, что необходимо строить график лишь вблизи точки -1; /0. При некотором практическом навыке

значения е и со, которые определяют 5Л/? Re[N(e.w)G(ju)]

автоколебания, могут быть получены в результате небольшого числа проб.

2. Точно такой же подход справедлив и при анализе с помощью семейства логарифмических частотных е=е

характеристик Л {е, со) G (Jd)). Значения амплитуды е и частоты со автоколебаний в системе соответствуют точке, в которой амплитуда равна 1 и фаза равна -л.

3. В некоторых случаях (в частности, когда N (е, со) действительное

число) удобно использовать корневой годограф функции NG (s). При этом следует найти те значения Л, при которых полюсы NG (s) расположены на мнимой оси.

Что касается первого способа, то иногда удобнее равенство (6.13) записать в виде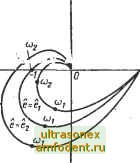

Рис. 6.6. Годографы, построенные по

функции N (е, о) G (/о) в зависимости от (О при трех различных значениях

амплитуды е

G(/co) =

N (е, (О)

(6.14)

и построить правую и левую части выражения (6.14) на плоскости G (/со). Функция в левой части дает обычную амплитудно-фазовую характеристику линейной части системы, в то время как функция в правой части равенства (6.14) определяет двухпараметрическое семейство кривых. В общем случае будет несколько пересечений кривых, соответствующих правой и левой частям. Прежде всего мы попытаемся определить те точки пересечения, которым соответствуют одинаковые частоты. Таким образом определяются

возможные частоты колебаний. Значения амплитуды е, определяемые правой частью уравнения, дают амплитуду колебаний. Такой метод удобен

лишь для простых нелинейностей N (е, со). Иногда пытаются показать, что изложенный нами способ является единственным для определения автоколебаний. Однако это просто неверно. В дальнейшем будут даны и другие способы определения амплитуд и частот автоколебаний.

в заключение отметим еще раз, что в нашем распоряжении имеется возможность анализировать автоколебания в системах автоматического управления. В дальнейшем везде будем предполагать, что точные условия возникновения автоколебаний в системе S определяют приближенные условия возникновения автоколебаний в системе S. В частности, комплексная величина N [е, со) называется эквивалентной передаточной функцией нелинейности Ш. В действительности, из-за того что нелинейность заменяется характеристикой, которая описывается в терминах усиления и фазы ,указанная процедура часто называется эквивалентной линеаризацией . Такое название, однако, не совсем точное, так как свойства аддитивности и однородности

при этом не соблюдаются *.

Пример 6.2. Найдем эквивалентную передаточную функцию для нелинейности типа насыщения, которая задается соотношением

Рис. 6.7. Эквивалентный коэффициент усиления для нелинейности, описываемой уравнением (6.15)

f(e) =

-е, -В<:е<В;

А, Ве;

-А, -В>е.

(6.15)

Обозначим входной гармонический сигнал через е sin и заметим, что если е меньше В,

то система работает в линейной области, а ее эквивалентное усиление равно отношению -g- .

Когда е превосходит В, то амплитуда выходного сигнала не более чем в -g- раз превышает

входную, но никогда не превосходит величины /4. Если е возрастает и далее, то выходной сигнал

приобретает прямоугольную форму с постоянной амплитудой А. Амплитуда основной частоты

2я . 4А .для прямоугольной волны с периодом -и амплитудой А равна-, что имеет место, ког-

да е -> оо. Эквивалентный передаточный коэффициент, таким образом, равен

которая

стремится к нулю. Значения эквивалентного коэффициента передачи изменяются непрерывно, как это показано на рис. 6.7. При этом эквивалентная передаточная функция не зависит от частоты, а из-за симметрии выходного сигнала также следует, что фазовый сдвиг ее равен нулю.

При входном сигнале е = е sin выходной сигнал и (t) равен е sin Ш,

(0 =

. В , .В

пл. - arcsm < < ил + arcsin

2пп + arcsin

at (2/г + 1) я - arcsin е е

(6.16)

(2п - 1) я -- arcsin

: Ш 2пл, - arcsin

п = 0, ±1, ±2, ... .

Для определения эквивалентной передаточной функции необходимо найти разложение Б ряд Фурье выходного сигнала и {t). Пусть

и {{) = 1 sin wH- 2 sin -f + Po -b Pi cos wH- Рг cos 2(i)t + -

(6.17)

* По этой причине и сам термин эквивалентная передаточная функция недостаточно оправдан. Отсутствие более удачной терминологии заставило переводчиков книги сохранить это название (Прим. ред.).