Определим (открытое) множество § как множество всех точек х таких, что Xi = Si, i = \, . . ., т, и, кроме того, х < х (и*, t. Множество § является выпуклым и представляет собой выпуклое множество, не имеющее общих точек со множеством G (t).

В нашем примере множество § рассматривается как полубесконечное пространство, определяемое Xi = и х <i х (и*, t). Поперечное сечение этого множества приведено на рис. 14.6, где через точку л: (и*, t) проходит плоскость, параллельная плоскости (хо, Xi).

Кроме того, определим множество § как множество всех состояний л: в пространстве где л:,- = s, при i = 1, . . , т, и, кроме того, Хд

Хо (и*, г)- Таким образом, множество § представляет собой множество § и его граничную плоскость Хо=Хо (й*, t). В нашем примере § представляет собой множество S и его граничную плоскость, определяемую х = Хд (и*, 2); = St.

В соответствии с определением множества G (2) и не имеют общих точек, так как в противном случае было бы нарушено предположение о том, что и* является оптимальным управлением.

Так как G (2) и выпуклы и не имеют общей точки, то существует по меньшей мере одна гиперплоскость, разделяющая их: т. е. множество G (/g) целиком располагается по одну сторону от этой гиперплоскости, а § целиком лежит по другую сторону. Вид этой плоскости с ребра показан на рис. 14.6. Фактически она представляет собой опорную плоскость множества G (t), проходящую через точку л: (и*, 2)-

Расстояние до плоскости от начальной точки определим как евклидовое расстояние г. Тогда внешняя нормаль ij к опорной гиперплоскости, направленная в сторону от G (t), обладает следующими свойствами: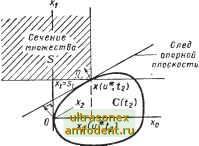

Рис. 14.6. Геометрия выпуклого достижимого множества, относительно множества G {t для особого класса систем, уравнения (14.43)

(xil)

Так как х (и*, t) принадлежит

~г, для всех л:£(3(2); >г, для всех х£8; г, для всех х§.

(14.46)

и к G{t) и к , имеем х (и*, t) 11

а это означает, что

{и*, tz) 11

llllll ~

(14.47)

(14.48)

Заметим, что любое перемещение точки л: (и* {t), параллельно оси х оставляет ее внутри множества § (где 2 - координата, которая остается свободной в момент времени 2)- Применительно к расширенному пространству п+х этот факт можно использовать для доказательства, что

r\i = О при i = т + \, . . ., п

и

т]о<0.

Пусть Bi представляет собой единичный вектор, параллельный i-й оси, тогда л: ( *, /g) + и л: ( *, 2) - принадлежат множеству при г = m + 1, . . ., п. Из соотношений (14.46) и (14.48) получим

{X( *, ,) + ецх(и*, U) 1] (14.49а)

(л:( *, 2)-eiYцх( *, 2) 1], г = m + 1, п, (14.496) а это означает

- 0<е1гК0

e?il = 0, (14.50)

что возможно только в том случае, если т],- = 0; г = m + 1, . . . , п.

Заметим, что л: ( *, 2) - принадлежит к множеству §. Поэтому в соответствии с соотношением (14.46) имеем

л: [и, h) - еоУ цх [и, h) ц; (14.51)

отсюда - воц О, а это означает, что

Теперь покажем, что если получены сопряженные векторы (0в соответствии с

4(0 - [Ф ( 2)]!] = Ч( t,)ri (14.52)

для 1 = 2. то можно доказать пункты 1) и 2) формулировки принципа максимума. В выражении (14.52) Ф (?, 2) представляет собой переходную, матрицу расширенной системы, а W (t, t,) - переходную матрицу соответствующей сопряженной системы.

Сначала можно доказать (см. упражнение 14.14), что

(t, tdg t)Yn{0- (t, t,)g{u, t)Yri, (14.53)

откуда следует, что

g{n, t)W{t,t2)ri>g4u, t)W{t, tri. (14.54)

С учетом выражения (14.52) запишем

g[{n, t)ip{t)g{n, t)ip{t). (14.55)

Добавив (A {t) X* it)y (t) к обеим частям неравенства, получим (А (t) X* (t) + ( *, t)f Я1,(t) (A (t) л:* (t) + g( , 0)4(0

H{x*, *, t, );H{x*, u, t, ij,) для всех teih, У, (14.56)

что представляет собой первую часть формулировки принципа максимума. Кроме того, из выражения (14.52) для всех t£ И t] имеем

= A.Wit, t,)n-A{t)W{t, 2)г] = -40(О- (14.57)

уравнение (14.57) представляет собой вторую часть формулировки принципа максимума. Оно показывает также, что (t) - сопряженный вектор. Кроме того, так как Ч? (2. 2) = I, то из выражения (14.52) следует, что 1] = 1з (2)- Таким образом, т]. = О при г = m + 1, . . ., п и т]о 0. Этим завершается доказательство условий 3) и 4) принципа максимума.

2. Доказательство принципа максимума в нелинейном случае

В общем случае доказательство оказывается значительно сложнее. Результаты, полученные для линейных систем, можно использовать применительно к общему случаю, если воспользоваться свойствами траекторий, граничащих с оптимальной траекторией.

В формулировке задачи, изложенной в п. 2 § 14.3, примем, что х(и*, t) представляет собой оптимальную траекторию в расширенном пространстве [сокращенно л:* (t)], ах (и, t) [сокращенно х (t)] обозначает траекторию, получаемую в результате применения любой другой допустимой функции управления u(f}. Разность бл: ( , t) х (fj-х* (t), называемую вариацией траектории и сокращенно обозначаемую как 8x(t), найдем из выражения

б.: = /(л:. и, t)~fix\ *, t).

Предположим, как и в гл. 5, что мы определили матрицу Якоби

-dfx dfx

Ж. дх

(х*, и*, t) =

дхп

и пусть

§()

g{u, t)Afix*, и, t)-fix*, *, t).

Тогда, подставляя бл: (t) =

дх дх

(t) и g [и, t), получим {t)T8x{t)+g{u, t) + h{x, и t).

(14.58)

/1{х, и, t) = fix, п, t)-f{x*, *, t)-g{u, t)-

1(0]*бл:(0.

Заметим, что h (х, и, t) будет мала , если будут малы векторы и (t) - -и* (t) и л: (О - X* (0.

Так как бл: (i) = О, то бл: можно точно найти, используя переходную

матрицу Ф [t, tj), соответствующую системе бл: = (t)

Ъх; поэтому

бл:( , 0 = i)l(b T)(g( , т) + А(л:, , т))т.

Предположим, что мы определяем приближенную вариацию бл:1 из системы

61 ( . 0=Г(0 8xi(t) + g(n, t).

(14.59)