Это означает, что вместо прежней линии переключения, которой была ось х формируется линия переключения в виде прямой

2 + axi = О,

(4.10>

имеющая наклон а. Последняя лежит во втором и четвертом квадрантах при а > О, как показано на рис. 4.7.

Траектории движения могут быть найдены путем интегрирования следующей системы уравнений:

Xl = хг, х = -U при х + axi 0; 1 Xl = х:, х = +f/ при х + axi < 0. j

(4.11>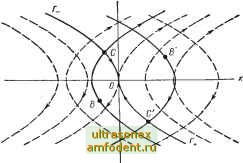

Линия переключений делит все фазовое пространство на две полуплоскости, в каждой из которых траектории определяются уравнениями (4.5) или (4.7). Сшивая отдельные части парабол, можно получить полную траекторию движения изображающей точки при произвольных начальных условиях. Выполняя эти построения, мы обнаруживаем, что в системе возникает скользящий режим (рис. 4.7).

Рассмотрим параболы, проходящие через начало координат, и, в частности, те их части, которые обозначены как Г. и Г . Линия переключения при а > О обязательно пересекает эти ветви парабол в точках Л+ иЛ соответственно. Поэтому существуют такие области начальных условий, при движении из которых изображающая точка, прежде чем попасть на линию переключения, пересекает линию Г = Г+ОГ . Сменив знак управления, изображающая точка пересекает ту же линию Г, но ближе к началу координат. И так происходит до тех пор, пока изображающая точка не окажется на линии переключения между точками Л и А. В этом случае, прежде чем попасть на линию Г, точка попадает на линию переключения. Сразу после переключения реле траектория будет опять направлена к линии переключения и реле переключится вновь. Таким образом, реле будет непрерывно переключаться, пока изображающая точка расположена на этой линии. В системе возникает скользящий режим *. Из физических соображений ясно, что и в скользящем режиме движение направлено к началу координат вдоль линии переключения. Таким образом, мы выполнили поставленную перед нами цель задемпфировать движение системы. Однако выбранный нами путь оказывается недостаточно эффективным.

С л у ч а й 6. Рассмотрим теперь схему, обеспечивающую оптимальное демпфирование в системе управления при любых начальных условиях (х, xq). Как и раньше, управление и (t) может принимать лишь значения +(/, -U или 0. Перенося траектории рис. 4.3, б, в на рис. 4.8, получим множество кривых. Заметим, что начала координат можно достичь лишь по двум из этих траекторий, обозначенных, как и на рис. 4.7, через Г. и Г .

Будем считать, что мы начинаем движение из некоторой произвольной точки В фазовой плоскости рис. 4.8. Наиболее разумным управлением для достижения начала координат будет управление и - -\-U, которое приведет вектор состояния системы в точку С на ветви Г . В этот момент управляющее воздействие следует сменить на к = -U, что заставит изображающую точку двигаться вдоль Г . В тот момент, когда изображающая точка достигнет начала координат, управление следует положить равным 0. Аналогичная стратегия лишь при обратных знаках управляющих моментов приведет изображающую точку в начало координат из точки В.

Из рис. 4.8 следует, что как только фазовая траектория достигает кривых Г. или Г . управление меняет знак, и дальнейшее движение к началу координат происходит вдоль этих кривых. Таким образом, в данном случае линией переключения является объединение кри-

Рис. 4.8. Траектории движения системы с оптимальным демпфированием, когда знак управляющего воздействия изменяется при пересечении с линиями переключения Г. и Г

* Частота и амплитуда этого дребезга (скользящего режима) на практике определяются динамическими свойствами неучтенных элементов системы. Если порядок рассматриваемой системы на самом деле равен двум, то частота переключений бесконечна, а амплитуда равна нулю. В этом случае говорят, что происходит скольжение вдоль линии переключерия.

вых Г. и Г . Такой способ управления позволяет провести изображающую точкуиз произвольных начальных условий в начало координат.

Если начальная точка (л;. х) расположена левее линии переключения, то выбираем управление w=+t/, которое сохраняется вплоть до попадания на линию переключения. Затем оно изменяется на и = -U, пока,изображающая точка не достигает начала координат; после чего управление полагаем равным к= 0. Если вектор начального состояния системы (Хщ. Хго) лежит правее линии переключения, то последовательность управляющих воздействий остается той же, но изменяется зндк этих воздействий. Уравнение линии переключения можно получить из уравнений (4.5) и (4.7) при с - О в виде

Uxxs +

= 0,

(4.12)

где (%s. х - фазовые координаты линии переключения. При этом управляющее воздействие в функции фазовых координат формируется следующим образом:

и = -и sign

Рис. 4.9. Реализация структурной схемы системы управления спутником Земли, обеспечивающая оптимальное демпфирование

-и, Хх>

2U 2U

(4.13)

С учетом ссотношения (4.13) уравнение (4.3) принимает вид Xi = Х2, Х2 = -и sign [f/Xj + х

(4.14)

Отметим, что спроектированная таким образом система с обратной связью не имеет входа. Поскольку ее поведение не зависит от времени, то это автономная система. Структурная схема такой системы показана на рис. 4.9.

Если управляющий момент ограничен величиной 11, то следует ожидать, что рассматриваемая система.есть в некотором смысле наилучшая система, поскольку в любой момент времени в нейреализуется предельный уровень управления. Как будет показано ниже, такая система управления является оптимальной в том смысле, что из любых начальных условий начало координат достигается за минимальное время.

Рассмотрение такого рода оптимальных в гл. 12 и последующих главах.

систем будет продолжено

4.2. СОСТОЯНИЯ РАВНОВЕСИЯ И ЗОНЫ РАВНОВЕСНЫХ СОСТОЯНИЙ АВТОНОМНЫХ СИСТЕМ

Как уже было показано в гл. 3, состояние равновесия Хе определяется из условия

л: = 0 при х = Хе. (4.15)

Для автономной системы второго порядка

Xi = /1 {Хг, хУ, Х2 = /2 (Xi, Х2) (4.16)

состояние равновесия определяется из условия

/1 (Xie, Хе) = 0; /2 (Xg, Хе) - 0.

(4.17)

Из примера 4.1 видно, что возможен случай, когда каждая точка некоторой линии является положением равновесия, т. е. существует целая зона равновесных состояний. Правда, в рассмотренном примере это имело место при некоторых исключительных условиях, когда м = 0. Однако и в ряде используемых на практике нелинейных систем такие зоны существуют. Рассмотрим два примера.

Пример 4.2. Так называемое кулоново трение приближенно описьшает действие силы трения на тяжелое тело, которое перемещается по некоторой плоской поверхности. Важ-ньм свойством характеристики кулонова трения является ее разрывная зависимость от скорости перемещения тела. Допустим, что система, изображенная на рис. 4.10, начинает движение, тогда ее уравнение движения при условии, что пружина и демпфер имеют линейные характеристики, можно записать в виде

х + ах + flgX + f (х) - 0; а, > 0..

(4.18)

Здесь нелинейная функция / (л;) характеризует кулоново трение. Если силой трения покоя можно пренебречь, то

>0;

I -с, л:<0,

где с - константа. При такой идеализации / (0) не определено, но из физических соображений ясно, что эта сила находится в пределах от -с до +с в зависимости от конкретных условий. Следовательно,

-с=/(0)с. (4.196)

В этом случае положениями равновесия являются все те точки, для которых выполняется условие ах f (0) = 0. Поскольку -с / (0) +с. то положения равновесия Хе должны

лежать на оси л; == О между точками х ---- к х =

Рис. 4.10. Механическая система (масса, пружина и жидкостное трение)

G(P)

Рис. 4.11. Схема нелинейной системы управления (к примеру 4.3)

Эта зона равновесных состояний на оси х I- обладает свойством устойчи-

и, и

являет-

вости. Допустим, что, находясь в указанной области, изменилась скорость х, став л;>0; тогда в силу уравнения (4.18) и соотношения (4.19) л:<(0 и скорость начнет уменьшаться, стремясь к нулю, т. е. к положению равновесия. Аналогичное явление имеет место, если возмущение л; < 0. На основании этого заключаем, что область <л; =0;---<Сх<С

ся зоной равновесия (см. упражнение 4.1).

Пример 4.3. Обратимся к системе, показанной на рис. 4.11. Б нее входят линейный элемент с передаточной функцией G (р) и нелинейный элемент с характеристикой / (е), причем / (е) = О при -б е б.

Если G (р) описывает линейную систему второго порядка с одним интегралом, то уравнения такой системы в нормальной форме будут

% = лгг; х = -ах + f (-JCi); / = % = -е.

В этом случае положения равновесия определяются из условия / (-х{) = 0. Последнее означает, что отрезок [х = 0; -б Jc :б} является зоной равновесных состояний.

Отметим, что, исключая время в уравнениях (4.16), можно получить дифференциальное уравнение только относительно переменных и х. Деля одно из уравнений (4.16) на другое, получим

dXi /2 (Л!, Х

(4.20)

Производная представляет тангенс угла наклона фазовой траектории к оси Xl. Из уравнений (4.17) и (4.20) следует, что в точках х, хе, соответствующих положениям равновесия, направление фазовых траекто-