ность п (п + 1)/2 функций Бремени, которые являются коэффициентами усиления в канале обратной связи. Применительно к нестационарным системам правильность получаемых результатов вызывает сомнение, и любая попьпка проверить полученный результат путем использования уравнения Беллмана может оказаться в высшей степени трудоемкой (см. упражнение 15.8). Далее, условие (15.51), являющееся по существу условием оптимальности для стационарных систем, накладывает исключительно жесткие ограничения, практически делая невозможным расчет сколько-нибудь слонжых систем..

В-четвертых, для систем с входным сигналом матрицу Р (t) необходимо вычислять, как н раньше, но, кроме того, функции времени <£} (t) и V (t) нужно определять, используя начение Z (t) в соответствии с формулами (15.69) - (15.72). Это значит, что мы должны знать будущие значения входного сигнала. Таким образом, данный результат невозможно использовать в случае совместной работы систем в режиме последовательного включения.

15.6. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ ДЛЯ СЛУЧАЯ, КОГДА ПРОИЗВОДНАЯ df* (х. t)/dx РАЗРЫВНА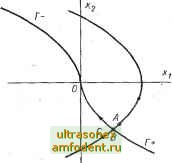

Рис. 15.4. Функция /* {х, f)=t* в примере 15..3 не является непрерывно дифференцируемой по X вдоль линии переключения Г±

В § 15.4 и 15.5 использовался частный случай уравнения Беллмана в виде (15.24). Как было показано в § 15.3-15.5, уравнение (15.24) можно легко использовать применительно к линейному объекту без ограничения на и и с критерием, представляющим собой интеграл от квадратичной формы по л: и й. Однако уравнение (14.24) выводится в предположении,

что имеет непрерывные первые частные производные как по лг, так и по t * Заметим, что даже в простой задаче, например, оптимального по быстродействию управления линейным стационарным объектом имеются области, в которых частные производные /* (л:, t) по х разрывны.

.Пример 15.3. Рассмотрим оптимальное по быстродействию управление объектом вида 1/р. Линия переключения показана на рис. 15.4 в виде кривой Г.

Величина f* в этом случае определяет минимальное время, необходимое для достижения начала координат. Вдоль траектории ABC эта величина изменяется, как показано на рис. 15.5. Таким образом, df*/dx не будет непрерьшной в точке В. В дальнейшем покажем, что df*/dx разрывна вдоль всей линии переключения Г (см. упражнение 15.4).

Заметим, однако, что в приведенном выше случае оптимальная траектория никогда не пересекает линию, вдоль которой функция df*/dx претерпевает разрывы.

В полуплоскости над линией переключения Г,. через {df*/dx). обозначается значение производной {df*/dx), которое она приобретает в том случае, когда приближение к линии переключения осуществляется сверху, тогда видно (см.. задачу 15.4), что если использовать (df*/dx)+ лишь в этой полуплоскости, то (5/*/бдс) непрерывна вдоль любой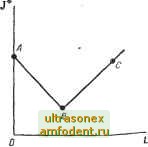

Рис. 15.5. Функция /* (х, f) = t* для примера 15.3 вдоль типичной траектории, пересекающей линию переключения Г+ (рис. 15.4). ТочкиА,ВиС соответствуют точкам этой траектории:

J* - значения функционала вдоль кривой ЛВС; 1--расстояние от точки А вдоль кривой АБС

1) В § 15.5 для того, чтобы связать функциональное уравнение динамического программирования с условием 1 принципа максимума, дополнительно требовалось существование и непрерывность второй частной производной функции /*.

оптимальной траектории. Аналогичный вьшод справедлив и для второй половины плоскости. Используя эти пределы, можно определить вдоль оптимальной траектории производную d (df*/dx)/dt, и она будет непрерывной.

Нам известно также, что в этом случае (df*ldf)- = О всюду; таким образом, уравнение Беллмана (15.24) будет справедливо, если соответствующий предел функции (df*/dx) существует.

Те случаи, в которых производная df*/dx претерпевает разрывы, подобно примеру 15.3, можно рассматривать с помощью более общего уравнения Беллмана (15.22). Заметим, что в предыдущем примере хотя производная df*ldx и является разрывной вдоль линии переключения, полная про-

изводная вдоль оптимальной траектории непрерывна (см.

упражнение 15.4). Действительно, если даже df*ldx и/ (х, и, t) не являются непрерывными на траектории х* (t) в точке л:* (т) то пока выполняется условие

[(1г) Z- = [(1г)/(-. . 0], (15.73)

величина

остается непрерывной при t = х.

Обоснованность уравнения Беллмана в общем случае доказана многими авторами, например, [18], [22] и [187]. При весьма общих условиях, которые выполняются для всех задач, приведенных в тексте, если при некотором управлении и* уравнение Беллмана справедливо вблизи линии или поверхности переключения, где df*ldx не определена, то и* представляет собой оптимальную функцию управления. Далее, если существуют односторонние пределы для производной df*[dx, то ее можно рассматривать как сопря женный вектор if во всем пространстве, где последний определен.

15.7. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ КАК ДОСТАТОЧНОЕ УСЛОВИЕ ОПТИМАЛЬНОСТИ

Из § 15.3 очевидно - уравнение Беллмана представляет собой необходимое условие оптимальности. Сформулируем и докажем теперь общую теорему, касающуюся метода динамического программирования.

Теорема 15.2 [187]. Рассмотрим систему, приведенную в § 15.3. Пусть область цели представляет собой множество §, а конечный момент времени не задан. Обозначим через открытую область, в которой функция V {х, t) определяется следующим образом:

1) dVldt непрерывна по л: и , а dV/dx или непрерывна по х и t, или удовлетворяет условию

ПтГ(

в любой момент времени t = х, когда dV/dx или / (л:, и, t) разрывны;

2) для каждого л: в в каждый момент времени t функция Гамильтона Я (х, и, t; dV/dx) имеет абсолютный минимум при ц = и* из множества допустимых функций управления. Кроме того, управление и* (t) определяет единственную траекторию системы х* (t);

3) на конечном множестве S V (х, t) = 0.

Тогда 1/(л:, t)=f*{x, f) при всех допустимых функциях управления, которые переводят изображающую точку из состояния лг в §, не покидая области Далее оптимальное управление с обратной связью и* {х, t) можно получить, решая соответствую.щее уравнение Беллмана.

Теорему 15.2 можно доказать следующим образом. В соответствии с условиями 1 и 2 теоремы можно написать

0 = f{x, 0+ и*, t) + L(x, u*,t)

<

<

{X, t) + [(

\Yf{x, u, t)-\-L{x, u, t)

(15.74)

Проинтегрировав левую часть (15.74) вдоль траектории л:* (О,от tx до оптимального конечного момента времени 4, получим

дУ{х*. t) dt

+ { fx fi *. t)]dt+\L{x*, a*, t)dt=.

где введенное обозначение

. dt J n*, t dV

dt+\L [x*, tt*, t) dt = 0,

Рассмотрим теперь интеграл

поясняется в § 15.3.

и*, t

(15.75)

==Иж+(1У/(л:, , t) + Lix, u,t)]

(15.76)

Далее допустим, что сочетание и* и л:* является единственным, которое доставляет абсолютный минимум величине W, равный в соответствии с условием (15.75) нулю. Если это утверждение неверно, то найдутся другие (t) ф Ф и* (t) ях (t) Ф л:* (t), которые сделают выражение (15.76) равным нулю. Однако из условия (15.74) следует, что подынтегральное выражение (15.76) всегда положительно. Таким образом, чтобы обратить W в нуль, указанное подынтегральное выражение должно равняться нулю на всем интервале 1, й]. Из условий (15.74) следует, что сделать это может лишь пара и* (t) их* (t). Таким образом, теорема 15.2 доказан-а.

Данная теорема служит обоснованием для всех рассмотренных в данной главе примеров.

Отметим, что слегка изменив условия задачи предыдущего параграфа, можно получить задачу, которую нельзя решить ни с помощью принципа максимума, ни на основе динамического программирования.

Пример 15.4 1). Снова рассмотрим объект вида = х; х = и. На этот раз используем показатель качества

f=\[x\ + xl+c\-)dt.

Примем далее ограничение и (/) 1. Если и (t) не имеет ограничения, то метод, изложенный в предыдущем параграфе, применим и можно найти оптимальное решение (см. пункт а упражнения !5.7):

{.t) = ~~{xj V\+2cXz),

Г15.77)

В работе [!87] имеются еще другие интересные примеры.