проводить синтез в частотной области, используя теоремы Парсеваля (см. приложение III). Функционал / в данном случае можно представить, используя преобразование Лапласа, в следующем виде:

/ [е (t), и (01 = J [е (t) + ku im di =

= I [E{s)E{~s)~-kU{s)U.{-s)]ds,

-/со

(12.9)

где E-{s) и и (s) - преобразования Лапласа от сигналов е (t) и и (f) соответственно. Введем обозначение

>--Rjs)-- l+Gi(s)G(s) (> =HH is)H sl]

тогда выражение (12.9) можно переписать в виде

flle{t),u{t)]flH{s)] = . J [Я(8)-1)х

X (Я (-S) - 1) + Цщ] (

(12.11)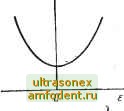

Рис. 12.2. ФунК1ия /е [Н* (s) ] в зависимости от е для малых е

Задача заключается в определении такой устойчивой передаточной функции Н* (s), которая минимизирует функционал / [Н (s)]. Чтобы найти оптимальную передаточную функцию Н* (s), -воспользуемся приемом, к которому часто прибегают при решении вариационных задач . Сначала заметим, что если Н* (s) - оптимальная линейная передаточная функция, то функционал / [Я* (s)] по определению должен принимать наименьшее значение, тогда для некоторой постоянной е выполняется следующее условие:

/ [Я* (S) ] < / [Я* (S) + гНу (S) ] = [Я* (S) ],

где Ну (s) - некоторая произвольная передаточная функция, не имеющая полюсов в правой полуплоскости переменной s. Теперь рассмотрим величину

/1Я*(8) + еЯ1(8)] = /,[Я*(8)]

как функцию от е. Для любой произвольно выбранной функции Ну (s) график [Я* (s)] от 8 для малых значений г будет иметь вид, показанный на рис. 12.2. Очевидно, что минимум достигается при 8 = 0. Будем считать, что /е [Я* (s) ] - гладкая функция от 8 при 8 = 0; тогда необходимыми условиями для существования оптимальной функции Я (s) являются

-/г[Я*(8)] = 0; (12.12а)

8=0

(12.126)

Из выражения (12.11) видно, что /е W* (s)] можно переписать в виде /8 [Я* (S)] =fa + 28/б + еУ (12.13)

* См. в гл. 13 более подробное изложение этого приема.

-/со

X /?(s)/?(-s)cfs =

(Я*(-5)-1)

ЙЯ* (-s) G (s) G (- )

/?(s)i?(-s)Hi(s)ds

и /с есть интеграл с неотрицательным подынтегральным выражением (по-

л D [Н* (s)]

кажите это). Взяв производную .-и приравняв ее нулю,

ц8 --

£=0

получим условие f = 0. Таким образом, для определения оптимальной передаточной функции Я* (s) необходимо, чтобы величина /j, была равна нулю для произвольной устойчивой передаточной функции (s). Итак,

,J 2nj

-/сх,

Кроме того, при положительном значении величины условие (12.126) выполняется. Так как мы предполагали передаточную функцию (s) устойчивой, то все полюсы функции Hi (-s) лежат в правой полуплоскости. С помощью теории функций комплексного переменного можно установить, что достаточное условие равенства нулю величины f состоит в том, чтобы полюсы, подынтегрального выражения в условии (12.14) были расположены в правой полуплоскости , Это, в свою очередь, означает, что полюсы выражения

G(5)G(-s)J

R{s)R{-s)

также расположены в правой полуокружности.

О учетом всего сказанного оптимальную передаточную функцию Н* ,{s) находим без труда. Читатель может сам убедиться в том, что изложенный выше порядок действий приводит к определению, оптимальной передаточной функции замкнутой системы Я* (s).

Теперь допустим, что функция А (s) не содержит ни полюсов, ни нулей в правой полуплоскости, и пусть

1+

A{s)A{-s) =

G (S) G (-s)J

Допустим также, что В (s) - функция, не имеющая нулей и полюсов в правой полуплоскости, для которой выполн.я тся соотношение В (s) В (-s)= = R (s) R (-s). И, наконец, допустим, что часть выражения в виде дроби В {s)/A (-s) запишется в виде В {s)/A (-s) = С+ (s) + С (s). Здесь слагаемое С+ (s) учитывает все полюсы в левой полуплоскости и половину полюсов, лежащих на мнимой оси. В этих обозначениях оптимальная передаточная функция Я* (s) запишется в виде

Я*(5) =

С. (S)

A(s)B{s]

(12.15)

Это можно показать путем интегрирования выражения (12.14) по контуру, который проходит по оси /со и полуокружности бесконечного радиуса в левой полуплоскости.

Как только Я* (s) найдено, передаточную функцию d (s) можно определить с помощью выражения (12.10). Найденные передаточные функции позволят определить минимальное значение функционала f в соответствии с выражением (12.11)

Рассмотренный выше метод является одним из наиболее удобных для практических расчетов. Причина этого заключается в том, что верхний предел интегрирования является бесконечным. Поскольку входной сигнал задан, а система линейна и стационарна, не представляет труда отыскать установившуюся реакцию системы и сократить процедуру оптимизации. Таким образом, в этом случае лишь начальные условия определяют решение, и мы, по существу, имеем дело с одноточечной граничной задачей, решение которой хорошо известно.

Однако предлагаемый метод не лишен и недостатков. Применение метода, как правило, приводит к тому, что спроектированная система имеет небольшой выброс, но ее реакция на малые изменения желаемого сигнала является вялой. Так, например, реакция на ступенчатый входной сигнал сильно затянута. Это явление обусловлено видом самого критерия качества (12.9), в котором большие значения сигналов е {t) и и (t) штрафуются в большей мере, чем малые. Однако, как будет показано ниже, всякая попытка видоизменить подынтегральное выражение, отказавшись от квадратичных составляющих, приводит к трудностям, которые нельзя преодолеть известными методами. Аналогичные осложнения возникают и в тех случаях, когда делается попытка изменить верхний предел интегрирования, сделав его конечным, или ограничить амплитуду сигнала и {t), тем самым переходя к нелинейной системе.

В гл. 15 будет показано, что ряд трудностей удается преодолеть, используя новейшие результаты; правда, при этом методы становятся более трудоемкими.

12.3. РЕШЕНИЕ ОПТИМАЛЬНЫХ ЗАДАЧ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ ДЛЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ

Анализ решения большого числа задач оптимального управления, для которых неприменим метод предыдущего параграфа, позволяет выделить два этапа. Во-первых, необходимо найти семейство решений, проходящих через две различные точки Ху и хК Решение, которое может претендовать на оптимальное, должно удовлетворять этим двум граничным условиям. Во-вторых, из найденного семейства траекторий, претендующих на оптимальные, необходимо каким-то образом выделить оптимальную траекторию.

Следующие четыре главы книги будут посвящены методам, которые и позволяют выбирать оптимальные решения. Прежде чем приступить к изучению частных методов, целесообразно рассмотреть последовательность определения семейства допустимых решений для оптимальных задач управления с закрепленными концами, описываемых линейными дифференциальными уравнениями.

В линейных системах задача определения семейства возможных решений значительно упрощается, поскольку для этих систем справедлив принцип суперпозиции, позволяющий получить такое решение, по крайней мере.

1 Вычисление интеграла (12.11) осуществляется с помощью таблиц (см., например, [ 150 ]). В системе управления, рассматриваемой в § 12.2, предполагается, что jCg устойчиво при t со.