Подставляя выражение (12.22) в уравнения (12.21), найдем уравнения линии переключения в виде

= 0 (12.23)

при и = -\-и.

Аналогично для и = -U имеем

(l h-.)-(l+x, -f-x) =0 при =-i/. (12.24)

Изучая эти уравнения, можно сделать следующие выводы. Во-первых, из уравнений (12.21) видно, что при положительных а и 6, когда объект управления устойчив, координаты I Xl (т) I и I Ха (т) I монотонно возрастают при увеличении т со все возрастающей скоростью. Отсюда следует, что все пространство состояний делится на две области линией переключения, а оптимальные фазовые траектории оказываются аналогичными траекториям изображенным на рис. 4.8. Все траектории в области с управлением -U неизбежно пересекутся с линией переключения + t/ и наоборот. Таким образом, для устойчивого объекта все его состояния полностью управляемы даже с \ и {t)\ U, и одного переключения и {t) достаточно для оптимального релейного управления.

Если один из параметров с или b отрицателен, то объект управления имеет по крайней мере один положительный корень. В этом случае можно считать, что не при всех начальных условиях будет обеспечено попадание изображающей точки в начало координат. Последнее легко показать, если воспользоваться канонической формой записи системы дифференциальных уравнений.

Пример 12.2. Пусть а>> О и & < О, тогда уравнения системы в канонической форме имеют вид

Xj = - oxj----= - o.Xi - . (12.25)

4 = - + -~Гь u = - bXi+v, 1 - .

где V =

При I и I 1 имеем I t) I -г- = V.

Оу - и

(у --а~

Н ~- ; при t) = -V координаты точки равновесия изменятся на + , - . Оба эти состояния - суть седловые точки, показанные на рис. 12.3, а и б.

Следует заметить, что при v =-V (или и = -1) существует только одна траектория, проходящая через начало координат; пусть это будет кривая Г (рис. 12.4). Аналогично при V = -\-V (или и = +1) кривую, -проходящую через начало координат, обозначим Г.

Итак, из сопоставления кривых на рис. 12.3, а и б можно видеть, что изображающая

точка из области, ограниченной линиями Хг = ± , переходит в начало координат

(см. рис. 12.4). Когда акЬ отрицательны, то множество начальных условий, из которых возможен переход в начало координат еще меньше, чем в рассмотренном случае. Последнее нетрудно показать (см. уравнение 12.6).

Способ обратного отсчета времени является крайне полезным при определении оптимальных законов управления для систем с линейными стационарными объектами, имеющими один вход *. Рассмотрим, например, си-

* Необходимо отметить, что пока нам неизвестны моменты переключения для попадания изображающей точки из начала координат в точку jCq, причем решение задачи в обратном времени не дает ответа на поставленный вопрос.

схему третьего порядка с действительными полюсами. Тогда, двигаясь из начала координат при управлении +U, получим траекторию Г+. Согласно теореме единственности (теорема 3.1) это должна быть единственная траектория, которая проходит через начало координат при управлении И, на-

Рис. 12.3. Фазовые траектории системы управления, описываемые системой уравнений (12.25), около положения равновесия: а - при с>0; b<0ho = -t-F;6 - при с>0, *<0ио = -V

оборот, при прямом отсчете времени конечный участок всех оптимальных Траекторий должен лежать на Г+. По аналогии с этим можно представить и траекторию Г , соответствующую -U и имеющую те же самые свойства (см. рис. 12.5).

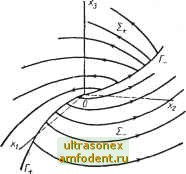Рис. 12.4. Оптимальные по быстродействию траектории для системы управления, полученные наложением рис. 12.3а и рис. 12.36. При начальных у

условиях I хо I !> -g- изображающие точки не могут быть переведены в начало координат

Рис. 12.5. Линии переключения и Г и поверхности переключения 2+ и S- для оптимальных систем управления по быстродействию с объектами третьего порядка

Пользуясь точкой Хг на кривой Г+ как начальным значением и обратным отсчетом времени, получим траекторию а {х, т) при управлении -U. Данная траектория обладает свойством: при прямом отсчете времени управление равно и = -и до точки х, а затем и = -\-U вплоть до начала координат.

Используя все точки на кривой Г+ для образования о при и = ~U, получим поверхность По аналогии с помощью кривой формируется поверхность 2+ (см. рис. 12.5). Отсюда ясно, что если объект управления устойчив, поверхности 2+ и S- делят все трехмерное фазовое пространство на две области. Эти области обладают тем свойством, что из любой точки одной из них управление и = +t/ переводит изображающую точку за некоторое конечное время на поверхность j]., а из любой точки другой области управление и = -и изображающая точка переводится на поверхность 2--Итак, если система третьего порядка устойчива, то максимальное число переключений для оптимального перехода в начало координат равно двум. Первое переключение происходит на поверхности переключения S+ или а последнее - на линии переключения Г+ или Г . Когда объект управления неустойчив, остаются в силе те же самые положения, за исключением того, что поверхности 2+ и 2- ограничены в пространстве. Поэтому не из любых начальных условий можно попасть в начало координат, но для тех точек, из которых можно попасть в начало координат, движение происходит с двумя переключениями.

Предыдущие рассуждения можно распространить на л-мерные системы с л > 3. Если гипотеза о релейном управлении верна, то для линейной стационарной системы п-го порядка с одним входом и действительными полюсами требуется не более п - 1 переключений полярности управляющей функции и {t) для перевода объекта управления из некоторого начального состояния в начало координат, если вообще такой перевод возможен. Строгое доказательство этого положения с использованием обычных методов довольно затруднительно.

Необходимо отметить, что для линейных объектов задачи оптимального управления сводятся к решению системы п алгебраических уравнений при условии, что происходит п - 1 переключений и известны полярности управления. В этом случае неизвестны только моменты переключений и полное время движения, а они и образуют п величин, подлежащих определению.

Можно установить и вид этих алгебраических уравнений. Для линейной стационарной системы с действительными полюсами элементы переходной матрицы Ф (t) представляют собой линейную комбинацию экспоненциальных функций. В конечный момент времени t* имеем

x(t*) = 0=Ф{t*)Xo+\ф{t*~:)bu{%)d%, (12.26)

так как Хо дано, а и (т) известны в течение всех п - 1 интервалов между моментами переключения t, t, . . ., tn i, то образуется система алгебраических уравнений относительно экспонент, показатели которых зависят от собственных значений, моментов переключения (f = 1, . . ., л - 1) и оптимального времени t*. Для системы, приведенной в примере 12.1,

-1 при О т <

+ 1 при tyx </*;

О при t* т,

. Затем, используя канонические координаты, получим систему алгебраических уравнений

и(х) =

решая которые, найдем время переключения ty и оптимальное время t*.