Корни уравнения (6.58) равны

bi;r + N,jE)+c4l-Ni,)Tj 2Tj{T+NxxTe) \ 1

[b {T + NiiTE)+a(\-Nxx)Tj\

(6.59)

Из условий задачи следует, что > 1; а > 0; Ь > 0; Г/ > 0; Г О и 0. Более того, из выражений (6.54) следует, что О ТУц 1 и Niio 0. Поэтому всегда справедливы следующие неравенства:

b(T+lN,.+a(l-Nn)TjO; ab(l-Nid+UoN2i>0.

(6.60)

Из соотношений (6.59) и (6.60) видно, что корни характеристического уравнения могут иметь лрбо нулевые, либо отрицательные вещественные части. Периодическое же решение возможно лишь в том случае, когда действительные части нулевые, т. е. при выполнении условия

! Ь{Т+NnTE) + ail-.Nxx)lTj=0. (6.61)

Этб условие будет вьшолняться, если величиной b можно пренебречь, а Мц = 1. Примем

Ь = О, тогда из выражений (6.54) следует, что существует область малых значений i, для которых Nil = 1 В этой области траектории системы имеют вид замкнутых кривых с центром

в точке равновесия (tg == to); (t; = vo). Вне этой области tojs - to и iVu < 1. Следовательно, Re X <; О и траектории имеют вид закручивающихся спиралей. Ясно, что в этом случае существует сепаратриса, разделяющая эти два движения. Все это поясняется фазовым портретом на рис. 4.22.

Если b Ф Q, то Из выражения (6.59) следует, что Re X О, и, следовательно, движение устойчиво. Однако метод гармонической линеаризации справедлив лишь для чисто мнимых корней, поэтому мы не будем предпринимать даже попытки анализировать результаты, когда Re X <; 0. Характерный для рассматриваемого случая фазовый портрет показан на рис. 4.21. Более подробный анализ поведения системы проведен в работе [88].

е.5. ИССЛЕДОВАНИЕ СКАЧКООБРАЗНОГО РЕЗОНАНСА МЕТОДОМ ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ]

-Метод гармонической линеаризации позволяет изучать поведение замкнутой нелинейной системы при определенном виде входного сигнала. Анализируя такие системы, необходимо помнить о том, что характер переходных процессов в них может быть чрезвычайно разнообразным. Если предположить, что управляющее воздействие синусоидально, то сигнал на выходе такой системы может:

1) иметь частоту, не зависящую от частоты входного воздействия автоколебания;

2) иметь период, кратный периоду входного сигнала, - субгармонические колебания;

3) иметь частоту, кратную частоте входного сигнала, - гармонические колебания;

4) не иметь определенной частоты - почти периодические колебания *;

5) иметь ту же частоту, что и входной сигнал, - вынужденные колебания.

Для большинства систем управления приемлем лишь случай 5. Тогда случаи 1 - 4 характеризуют нежелательное поведение системы, но ин-

* Почти периодические колебания возникают, например, в системе, которая находится на границе автоколебаний, когда частота входного сигнала и частота автоколебаний не пропорциональны; такие колебания не имеют определенной частоты, хотя на первый взгляд кажется, что эти колебания периодические (см., например, [72]).

женер всегда должен помнить о таких случаях, чтобы избежать их появления на практике. Вообще говоря, случаи 1 )- 4) имеют место, лишь когда соответствующая свободная система находится на границе автоколебаний. Случай 2, например, характерен лишь для систем, период автоколебаний которых кратен периоду входного сигнала, тогда как случай 3) связан с тем, что частота автоколебаний кратна частоте входного сигнала. Поведение первого типа присуще только осциллятору.

Замкнутая система, включающая линейный объект и простую нелинейность, может находиться на границе устойчивости по двум причинам. Объект третьего порядка и выше может проявлять тенденцию к колебаниям из-за

наличия в контуре нелинейности или из-за того, что объект имеет на некоторой частоте резонансный пик. Если инженер предостерег себя от этих двух возможностей, то, как правило, частота выходного сигнала соответствует частоте входного. И все-таки даже в этом случае возможен еще один тип аномального поведения нелинейной системы. Это явление скачкообразного резонанса.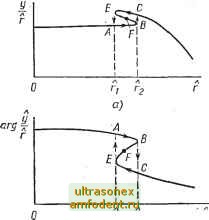

r(t)

y(t)

П Г2

Рис. 6.16. Явление скачкообразного резонанса в нелинейной системе

Рис. 6.17. Простейшая одноконтурная структурная схема нелинейной системы управления для исследования явления скачкообразного ре- зонанса

Если у - амплитуда первой гармоники выходного сигнала, а г и со - соответственно амплитуда и частота входного синусоидального воздействия, то явление скачкообразного резонанса заключается в следующем (рис. 6.16).

При фиксированном со, когда г медленно возрастает, отношение плавно

изменяется вплоть до г, затем наблюдается скачок в значении у/г. Точно такое же явление обычно наблюдается и на фазовой характеристике, как это показано на рис. 6.16.

Когда амплитуда г уменьшается от значений, больших г2, то скачок

происходит уже при амплитуде г. Обычно меньше, чем г,. Явление скачкообразного резонанса можно наблюдать также и пркизменении лишь частоты входного сигнала. В этом случае соответствующие характеристики амплитуды и фазы как функции частоты подобны изображенным на рис. 6.16, а, б.

Явление скачкообразного резонанса во многих случаях можно проанализировать методом гармонической линеаризации при условии, что предприняты меры для предотвращения явлений 1) - 4), о которых метод гармонической линеаризации не несет никакой полезной информации.

В этом параграфе мы рассмотрим лишь случай системы, содержащей нелинейность типа насыщения. Структурная схема такой системы показана

на рис. 6.17, где входное воздействие г (t) = г sin со и нелинейность %

имеет единичный уровень ограничения (§ 6.2). Сделаем следующие предположения-:

1. В системе не возникают субгармоники.

2. Частотная характеристика G (/со) соответствует устойчивому объекту и хорошо фильтрует высокие частоты.

3. При отсутствии входного сигнала замкнутая система устойчива. При таких предпосылках метод гармонической линеаризации должен

дать достаточно точную оценку вынужденных колебаний.

Пусть входной сигнал г (t) = г sin (со/ + 6), а первые гармоники установившихся значений е (t) и у (t) соответственно равны е sin (со/ + б) и

ImG(jcj)

ReG(jcj)

Треугольник при ё~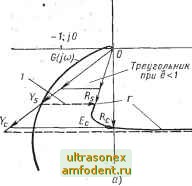

Рис. 6.18. Построение Лозьера на плоскости G (/м) для выявления скачкообразного резонанса в системе управления с нелинейностью типа ограничения:

а - при е - 1 (система управления работает в линейной части нелинейной характеристики); б - е > I (система управления работает в области насыщения нелинейной характеристики)

г/sin (со/+ Ф). При исследовании явления скачкообразного резонанса в такой системе целесообразно использовать подход, предложенный Лозьером [128]. Если предположения метода гармонической линеаризации выполняются

/? (со) = £ (со) + К (со), (6.62)

где /? (со), Е (со) и К (со) - векторы, соответствующие гармоническим сигналам г (t), е (f) и у (t). Примем за вектор отсчета Е (со), тогда б = О и указанный вектор параллелен действительной оси. Теперь не представляет труда определить условия скачкообразного резонанса, воспользовавшись геометрическим построением на плоскости G (/со). Если б = О, то фаза вектора V равна фазе G (/со); используя принятые обозначения, получим

arg К = arg [G(/co)]. (6.63>

Проведем геометрические построения, когда изменяется амплитуда е.

Если е = 1, то это соответствует достижению уровня насыщения. При этом векторы У и О (/со) совпадают. Условие (6.62) определяет треугольник векторов, показанный на рис. 6.18, а. Такое построение проводят прямо на плоскости G (/со), используя годограф частотной характеристики G (/со).

При е < 1 система работает в линейной зоне; в этом случае треугольник

построения подобен треугольнику векторов для случая е = 1 (рис. 6.18, а)