Таким образом, можно получить другую кривую (у), пользуясь точками пересечения кривых {&) (с у в качестве параметра) с линией ImJ2(00) = К. Пересечение кривых cd (у) и coj (у) определяет искомые значения величин ©о и 7i.

Пример 8.4. Рассмотрим систему управления, изображенную на рис..8.1 при г = 0. Реле имеет характеристику, показанную на рис. 8.2, б, с параметрами U = 1; £ = 0,2; К = = 0,1. Линейная часть системы описывается передаточной функцией вида

G (р) =

р(р-м)

1т Jlcj)

-o.fi -0.6 / тГу-о.г X

Рис. 8.8. Годограф Цыпкина для системы управления с реле . с зогюй нечувствительности и гистерезисом (пример 8.4): (со) и /а (и) - семейства годографов для различных значений у

ImG(Ju)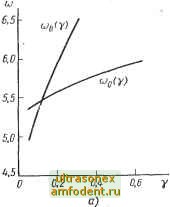

Рис. 8.9. Определение соо: а - с помощью кривых со (т) и coj {у); б - с помощью эквивалентной передаточной

функции

Требуется определить частоту колебаний и соответствующую величину параметра 7, и сравнить эти величины с полученными на основе метода эквивалентной передаточной функции.

Годографы Цыпкина для системы управления построены на рис. 8.8 *. По пересечению-кривой Jl (со) с линией Im/jL (со) = -8 и кривой (со) с линией Im (со) = X определяем графики сОд (у) и соь (7). Эти графики построены на рис. 8.9, а; далее находим, что = 5,5-и 7i= 0,1.

Обратная эквивалентная передаточная функция построена на рис. 8.9, б, где также показана амплитудно-фазовая частотная характеристика. Так как нелинейность имеет гисте-/ 1 \

резне, то функция---имеет фазовую характеристику, зависящую от амплитуды е.

\ N{e)J

Поэтому характеристика (е) имеет действительную и мнимую части вида

Re N (е) -

Im N {е) =

Из рис. 8.9, б находим coq 5,5 рад/сек и е я 0,36. Отметим, что частота автоколебаний, полученная упрощенным методом, совпадает с ранее вычисленьюй частотой. Однако величина амплитуды автоколебаний ео является нереальной (так как при этом 70 составляет 0,6). Пользуясь значением у о, полученным по кривой Цыпкина, по соотьюшениям (8.56) определяют истинную величину основной составляющей вд (О = -уп (О, равную 0,2.

Таким образом, определение параметров предельного цикла, основанное на методе эквивалентной передаточной функции, может привести к неверным результатам при анализе некоторых систем управления.

8.5. ДРУГОЙ СПОСОБ ПОСТРОЕНИЯ ГОДОГРАФА ЦЫПКИНА

В этом параграфе будет найдена простая зависимость между J (со) и z-преобразованием передаточной функции линейного элемента. Это позволит отказаться от суммирования бесконечных рядов.

Ограничимся рассмотрением случая реле без зоны нечувствительности, хотя это можно сделать и для реле с зоной нечувствительности. До сих пор в этой главе не требовалось, чтобы линейный элемент был устойчивым. Однако в этом параграфе введем ограничение на передаточные функции G (s) и Fo (s), требуя их аналитичности при Re s О, за исключением может быть, простого полюса при s = 0. Проанализируем только симметричные колебания.

Как и раньше, положим

G{s)

Тогда для основного тона колебаний, начинающихся при t = -NTy

можно воспользоваться выражением (8.11 а), где а =и Т= и записать

и it) = \imU У (-1) Li (t-k)~ i\t-{k+\)-]}. (8.59)

k=-N

* Поскольку требуется знать лишь значения годографа Ji (со) вблизи величины (-е),. а годографа (со) вблизи величины X, то необходимые вычисления можно существенно сократить и использовать для вычисления сумм (8.58) настольные вычислительные машины.

Переходная характеристика линейного элемента и ее производная в момент времени при - - принимают следующие значения :

-Ч<-*>Ш )])+ Ш-

= j,(oo)-2u]h1)*(*.5.)++2( .(0+); (8.60а)

у{)=к (оо) - 2V (-1) + 2Ug (0+). (8.606)

Поскольку мы предположили, что Fo () и G (s) - аналитические функции в Re S О, за исключением возможно простого полюса при s = О, то существует предел, функции у о (оо) и у (оо), и он равен нулю. Кроме того, Б силу (8.3) имеем h (0) = 0. Сходимость бесконечных рядов (8.60) становится очевидной, .если их переписать в следующем виде:

(0+) -lim Г (2)

(8.61)

где (z) и (z) представляют собой z-преобразовання функций h (t) и g() С выбранным интервалом или -. Таким образом, получим

S ) = S

(8.62)

/г=0

Функции Н (s) я G (s) - аналитические в области Re s Q, за исключением, быть может, точки s= О, поэтому их z-преобразование является .аналитической функцией в области \г\ 1, исключая, возможно, точку Z = +1- Таким образом, пределы функций ffe (z) и g (z) в соотношениях (8.61) при Z ->-1 существуют и обеспечивают сходимость ряда (8.59).

С учетом выражения (8.61) функция Цыпкина, определенная формулой (8.44), равна

У (со) = (-]) (0]] -f / {2Vm (-1) -Уо (х)]. (8.63)

Поскольку функции (z) и (z) зависят от со, то и выражения (-1) и (-1) зависят от со. Для того чтобы их зависимость от со стала явной, следует при записи соотношения (8.63) использовать импульсные передаточные функции G* (s) и Я* (s), период дискретности которых

равен - . Эти функции равны

(S) = [ехр ()] ; Я* (s) = [ехр ()

(8.64)