где Q я R- симметричные, положительно определенные постоянные матрицы, справедливо условие lim/ (7. = О и,.таким образом, матричное

Г-Уоэ

уравнение Риккати (15.46) сводится к нелинейному матричному алгебраическому уравнению

(15.49)

-PBRTBP + РЛ + АР + С? 0.

Решение этого уравнения определяет постоянную матрицу Р. Оптимальное управление имеет вид и {х, t) = -R~BPx. Приведенный выше результат совпадает с результатом, полученным в § 13.2, хотя все требуемые свойства можно получить и непосредственно из уравнения (15.49).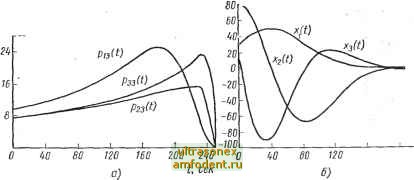

m 200

1,сек

Рис. 15.2: о) Оптимальные функции усиления обратной связи для системы, рассматриваемой в примере 15.2; б) оптимальная траектория для системы, рассматриваемой в примере 15.2

Уравнение и* (х, t) = -R~BPx означает, что все переменные состояния должны быть известны. Это означает, что должны точно измеряться выходной сигнал и (п - 1) его производная. Это очень жесткое требование.

По существу, применительно к случаю одного управляющего воздействия Калман [97] показал, что если в приведенной выше задаче уравнение (15.49) определяет постоянную матрицу Р, получается строгое решение в частотной области.

Пусть объект, определяемый уравнением х = Ах Ьи, полностью управляем (см. § 3, 6), а показатель качества имеет вид

{хЦ1) Qx{t) + mHt))dt,

* Т Т

управление - суть и = -(1/г) b Рх = -k х, когда к = ЬР/г. Тогда передаточная функция разомкнутой оптимальной системы управления равна (см. § 3.5)

а оптимальное

r{s)=k (sI - Ar Ь.

(15.50)

Предполагается, что Q является положительно определенной, а г > 0.

Покажем, что функция (s) обладает тем свойством, что при всех частотах ш

1 + *(/ш)>1. (15.51)

Для доказательства заметим, что в нашем случае

при этом / можно нормировать так, что г = 1.

Таким образом, уравнение (15.49) принимает вид i>

~PA-AP=Q - PbbP. (15.52)

Прибавляя и вычитая sP, получим

/>(8/ - Л) + (-8/ - Л)/>=е -(15.53)

Передаточна! функция объекта от и до л: определяется выражением Н(&) = (s/ -Л)-! Ь.

Если обе стороны уравнения (15.53) предварительно умножить на

tf (-s), а затем на Н (s), то найдем

(-S) РЬ + ЬРН (S) = (-S) \Q - РЬЬР\ Н (S)

(-S) РЬ + (-S) PbbPH (s) + г;>Я (s) = (-s) (s), (15.54)

так как положительно определенную матрицу Q можно представить в виде

Q = DKD,

где матрица D - действительная, а матрица Л - действительная, положительно определенная и диагональная

Уравнение (15.54) можно записать (с учетом того, что k = РЬ) следующим образом:

[\+H\-s)k)[\+kH{s)) = \H\-s)DADH{s). (15.55)

. Ввиду того, что kH (s) = F (s), имеем при s = уш

\l+F* (/со) Р 1 -Ь (-/ш) DADH (/ш). (15.56)

Так как последний член уравнения (15.53) всегда положителен, то условие (15.51), очевидно, выполняется. Его можно представить в виде единичной окружности с центром в точке -1 + /О, которую годограф F* (/со) не должен касаться или входить в нее. Это значит, что какой бы ни была первоначальная передаточная функция объекта G (s), оптимальный линейный регулятор путем компенсации будет превращать ее в F* (/со) с указанными выше свойствами. Нет необходимости говорить, что вследствие строгости условия (15.51) оптимальное управление трудно будет осуществить в случае нетривиальных управляемых объектов.

Хотя приведенные выше результаты применимы лишь к системам без элемента сравнения, их можно очень легко распространить на системы

) В случае одного управляющего воздействия вектор R в уравнении (15.49) переходит в скаляр г.

2) См. работу [12]. .

с элементами сравнения и входными сигналами, принадлежащими к какому-то определенному классу.

Рассмотрим линейный стационарный объект с одним входом и выходом, -определяемый уравнениями х = Ах + Ьи и у = сх.

Обозначим через z (t) входной сигнал, поступающий на элемент сравнения. В частности, желательно найти такую функцию управления и, чтобы минимизировать функционал

/ = j (9 (О + ru (0) dt, . (l5.57)

где eit) = z (t) - у (t).

Ввиду того, что функция Z (t) зависит от времени, следует ожидать, что управление и (х, t) будет нестационарным даже в том случае, когда верхний предел интегрирования в показателе качества равен бесконечности и управляемый объект является полностью управляемым и наблюдаемым (см. § 3, 6), и описывается передаточной функцией G (s) = [М {s)/L (8)] или операторным уравнением L (р) у (t) = М{р) и (t) (см. §2.3). Если z (t) подчиняется соотношению

L (р) z{t) = 0, . (15.58)

то можно написать

L (р) е (t) = -М (р) и (0; . (15.59)

последнее можно рассматривать как уравнение эквивалентного объекта -с входным сигналом -и (t) и выходным сигналом е (t). Можно выбрать подходящий набор переменных состояния, чтобы охарактеризовать эквивалентный управляемый объект (15.59) (например, е () и ее п - 1 производных). Таким образом, задачу, рассмотренную в § 12.2 в частотной области, теперь можно полностью рассмотреть во временной области.

15.5. СВЯЗЬ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ С ПРИНЦИПОМ МАКСИМУМА

Внимательный читатель, возможно, обратил внимание на заметное сходство выражений (15.22) или (15.24) и выражения, связанного с максимизацией функции Гамильтона в формулировке задачи оптимального управления на основе принципа максимума. Так как для любой функции F шах (-F) = = -min F, то выражение (15.24) можно записать в виде

= max

~L (х (и, t), и, t) - [Щр /] . (15.60)

Если вдоль оптимальной траектории вектор -df*ldx отождествить с сопряженным вектором -ф, то величина, заключенная в квадратных Скобках в уравнении (15.60), является гамильтонианом Я для принципа максимума. Заметим, что в этом случае величина df*ldt представляет собой величину Я (л:*, и*, t, 1) и выполняется условие 2 принципа максимума (теорема 14.3) (см. упражнение 15.13). При этих условиях имеем

-чКО; (15.61а)

. = Я* = Я(л:*, и*, t, ф). (15.616)