Решение свободной системы 2 (п - 1)-го порядка можно легко определить. С учетом результатов § 13.2 видно, что собственные значения этой системы снова необходимо симметрично разместить относительно мнимой оси комплексной плоскости. Действительно, характеристическое уравнение имеет вид

S (- кУ~к~Я1 = 0; (16.26)-

его собственные значения; Kk и - Я. Предположим теперь, что отличаются друг от друга.

Выберем (п - 1) значение корней Я;, причем Re < О для каждого значения. Это множество корней является решением для приведенной выше системы 2{п - 1)-го порядка вида . .

/=1

(16.27)

Система (16.27) содержит n - 1 произвольных постоянных k, . . ., ki зависящих от конкретного решения. Эту систему можно охарактеризовать и по-другому, написав уравнения (16.27) в виде

(16.28}

где представляет собой постоянный я-вектор. Из уравнений (16.27) и, (16.28) следует, что с определяется (почему?) выражением

(16.29)

Решение системы уравнений (16.27) будет сходиться к началу координат, так как ReA,y,<0 для j = I, . . ., п-1 и, следовательно, оно может быть использовано для оптимального решения. С помощью последнего уравнения (16.22) можно найти такое и (t), которое в состоянии сохранить решение на гиперповерхности, определяемой уравнениями (16.27) и (16.28). В соответствии с материалами § 13.2 управление и можно выразить в форме

и{х) = <Гх. Далее учитывая уравнение (16.22), имеем

п-1 п

(16.30)

n-l n

djX = - S uik

1=1 i=\

(16.31)

при конкретном выборе Я и, следовательно, и{х) (поскольку вырожденная гиперповерхность образуется, по существу, свободной системой) по теореме единственности следовало бы ожидать, что на этой гиперповерхности функ-

иионал / зависит лишь от начального и конечного состояний. Теперьконечным состоянием является начало координат О, которое, как мы видим, также находится на вырожденной гиперповерхности. Таким образом, на этой гиперповерхности через каждую точку проходит единственная траектория, которая в конечном счете приводит к началу координат.

Если можно установить, что лучшего пути перемещения изображающей точки по вырожденной гиперповерхности в начало координат нет, то опти-мальйость вырожденного управления, определяемого уравнением (16.30), обеспечена. Это доказали Уонхэм и Джонсон, показав, что значение / , определяемое уравнением (16.30) для точек на вырожденной гиперповерхности, невозможно улучшить.

Оптимальное решение для начальных состояний, не находящихся на :вырожденной гиперповерхности, будет включать в себя управление и*, которое равно +1 или -1 до тех пор, пока не будет достигнута вырожденная гиперповерхность. Следует отметить, что в зависимости от того, где оптимальная траектория встречается с вырожденной гиперповерхностью, функция и может иметь или не иметь разрывности при достижении гиперповерхности.

Отметим также, что в то время как в примере 16.5 функция sign О давала значение, равное нулю, то в данном случае, ввиду того, что управление и (х) является линейным,- функция sign О дает значение, непрерывно изменяющееся в пределах от +1 или -1 до 0.

Пр и м е р 16.7. (Уонхэм и Джонсон). Пусть управляемый объект имеет вид x-Xz; хи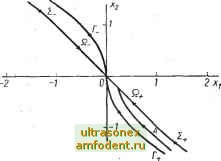

Рис. 16.5. Различные области оптималь-.ного управления для системы, рассматриваемой в примере 16.7

2 J О

в соответствии с каноническим уравнением

xi = х; Х2 = и; ii = xi, = -+ 2

(16.32)

;и принципом максимума имеем и* = sign ifa всякий раз, когда ifa Ф 0.

Если ifig ф О, то уравнение (16,32) дает ijjg = О = - Ь х, а следовательно, х = ifi-Тогда первое и третье уравнения (16.32) дают

X, = ifi; ifi = Xi- (16.33)

Система (16.33) эквивалентна xi- х, ~ 0; в этом случае собственньми значениями уравнения (16.33) являются /-1 = -1; = +1. Кроме того, из соотношения (16.31) получим d, = = 1; dg = 0. Таким образом, с помощью уравнений (16.29) и (16.30) найдем уравнение для всех вырожденных траекторий в следующей форме:

Xi+X2=0; >ill, (16.34)

которое представляет собой отрезок прямой линии, проходящей через начало координат. На рис. 16.5 это показано в виде отрезков й. и й .

. Линии 2+ и 2- представляют собой соответственно траектории, полученные управле-.нием ы = 4-1 и ы = -1 и проходящие через точки (1; -1) и (-1; 1).

На множестве (16.34) (т. е. на множестве й ) оптимальное управление является линейным:

. u*(x) = xi. (16.35)

В других точках оптимальное управление является релейным, и все результирующие траектории, за исключением двух, будут пересекать или отрезок й,или линию переключениях-Этими двумя исключениями являются релейные траектории, проходящие через начало коор-динати обозначенные на рис. 16.5 как Г. и Г . Таким образом, для всех начальных состоя-

ний; не лежащих на Г , часть оптимальных траекторий будут вырожденными. Типичной траекторией этого типа является траектория Л на рис. 16.5. Оптимальнымуправлением для этой траектории является +1 до достижения линии Q.. Так как линия Q+ пересекает траекторию в точке с координатой Xi меньшей единицы, то в соответствии с выражением (16.35) в точкг пересечения и* (t) претерпевает скачок.

Известно также много примеров вырожденных управлений для нелинейных систем. Наиболее известной, вероятно, является задача ракеты - зонда (см. упражнение 16.6). В этой задаче для достижения ракетой максимальной высоты не всегда требуется программирование величины тяги.

16.5. СВОЙСТВО ВЫРОЖДЕННЫХ РЕШЕНИЙ

Исследовав некоторые проявления особенностей решения, будет полезно рассмотреть теоретические аспекты этогокласса задач. .

Мы уже отмечали, что в случае вырожденного управления наблюдается неясность при удовлетворении принципа максимума, такая, например, как sign О, которая не определяется. Целесообразно исследовать особый случай в отношении других необходимых условий оптимальности.

Для простоты рассмотрим типичную задачу с одним управляющим воздействием и. Заметим далее, что в классах задач, рассматривавшихся до сих пор в данной главе, управляющее воздействие и появлялось в задаче линейно, т. е. уравнения системы можно написать в виде

x = fix,t) + gix,t)u, (16.36)

а критерий оптимальности может быть представлен в виде

=\ifo{x,t)go{x,t)u)dt. (16.37)*

Кроме того, в каждом из рассмотренных классов задач на и (t) накладывается ограничение

\u(t)\U. (16.38)

Сформулируем теперь эту задачу на основе метода, приведенного в § 13.5 **. Соответственно функции v {t} и {и, v) определим в виде

е (и, V) = (и (t) + U){U~u (0) - v40 = О . (16.39) и далее найдем множители if и v и образуем

L2{x,x,iS,u,v,%,Q = U{x,t) + go{x,t)u)-ir

+ (x-f {X, t)-g {X, t) и) + К {и, V). (16.40)

Предположим, что мы проверяем выражение (16.40) в отношении условия Лежандра-Клебша [см. уравнение (13.53)] dLJdu О, тогда получим

=-00. (16.41)

* Для управления, оптимального по расходу топлива, подынтегральное выражение для показателя качества представляет собой функцию \и\. Однако напомним, что для этого класса особое управление имеет место только для тех и (Q, которые не изменяют знака. ** Предполагается, что эта задача не является вырожденной.