где, как это следует из уравнения (15.49), матрица Р имеет вид

/1+2с с

(15.78)

с 1/1 + 2с.

Однако в том случае, когда на и {t) накладывается ограничение типа неравенства, задача становится более сложной. Решение (15.77) будет справедливо внутри области, т- е. когда и* () не принимает граничных значений. Исходя из этого многие авторы предполагали, что для рассматриваемой здесь задачи оптимальным решением будет управление вида и* (f) = = sat [(-1/с) (х, - Kl + 2с Xg)]. Однако, как показано ниже, это решение является неверным.

если

Рис. 15.6. Области различных оптимальных управлений для системы, рассматриваемой в примере 15.4;

S - область линейного управления; Т) - области управления; за пределами S н Т) оптимальным является релейное управление

Уравнение Беллмана для этого примера принимает вид (см. упражнение 15,7)

и и* {х) равно

и* (дс) == sat

с дх2 J

(15.79) (15.80).

что дает точное решение, за исключением того, что df*ldx заранее неизвестна.

Функция управления вида (15.77) является, несомненно, оптимальной, если она никогда не превьш1ает предела, устанавливаемого ограничением. Все состояния, соответствующие такому управлению, определяют область, где линейное управление (15.77) является оптимальным. Можно заметить, что эта область S ограничена двумя линиями, для которых и* (t) = ±1 или

(15.81)

~~{x,-i-Vi + 2cx2)= ±1.

и двумя траекториями, соответствующими управлению и = ±1, и касательными к этим линиям. Область показана на рис, 15.6.

sat [х] =

Г+1. х>1 х. ilscl; - 1, -1.

Однако сейчас нельзя сделать вывод, что за пределами области требуется релейное управление, так как могут быть и другие области, в которых аргумент функции (15.80) принимает значения меньшие единицы.

Для нахождения других областей, где требуется решение, отличное от линейного, нужно проследить за оптимальной траекторией при обратном течении времени, начиная от границы. Для этого найдем сначала канонические уравнения, исходя из принципа максимума. В данном случае этими уравнениями являются

. Г 1 = л: ; х, = sat

-яр2 (О

(15.82)

*i = :i; ф2 = л:2--ф!.

Так как для начальной точки в области S справедливо в соответствии с уравне-ииями (15.82) соотношение /* (х, t) = {}1хРх, то в этой области

\--=~Ц-Рх. (15.83)

Обращая время в уравнениях (15.82) и используя в качестве начальных состояний точки на границе области 5, можно, проанализировав оптимальную траекторию, найти области, где оптимальное управление подчиняется условию и* < 1.

Результат, полученный Джонсоном и Уонхэмом [87], показывает, что управление удовлетворяет неравенству и* К 1 также в области г), изображенной на рис. 15.6. Если область ц имеет нелинейные границы, то ясно, что управление вида и*(дс) =sat ((-1/с) (х, - 11 + 2сх] не дает правильного решения. К сожалению, точная форма границы для области rj до сих пор не определена.

За пределами области и г\ управление и* является релейным, как показано на рис. 15.6.

15.8. КРАТКОЕ СОДЕРЖАНИЕ

Достоинство метода динамического программирования, предложенного Беллманом, состоит в том, что основные функциональные уравнения [уравнения (15.22) и (15.24)] достаточно просто выводятся на основе принципа оптимальности, согласно которому любая часть оптимальной траектории (и связанная с ней функция управления) должна быть оптимальна.

Основное функциональное уравнение, обычно называемое уравнением Беллмана, представляет собой нелинейное дифференциальное уравнение первого порядка в частных производных относительно критерия оптимальности /*. Это уравнение представлено в форме (15.24). Граничное условие задается в одной точке. В общем случае уравнение справедливо во всем пространстве состояний, за исключением, возможно, линии или плоскости переключения. Более общая форма уравнения Беллмана, которая справедлива во всем пространстве состояний данной задачи, определяется уравнением .(15.22).

Для того чтобы на основе метода динамического программирования вывести условия оптимальности, полезно мысленно представить себе поверхность функции /* в п-мерном пространстве переменных х.

Динамическое программирование удобно использовать при решении оптимальных задач для линейных систем управления, когда показатель качества представляет собой интеграл от суммы квадратов переменных хяи (§ 15.4). При решении других задач динамическое программирование менее эффективно в сравнении с принципом максимума, поскольку требуется решать дифференциальное уравнение в частных производных.

В тех случаях, когда df*ldx не является непрерывной по х, используется общая форма уравнения Беллмана - уравнение (15.22). К уравнению (15.22) обычно приходится обращаться в том случае, когда на функцию управления и (t) наложены ограничения типа неравенств.

Довольно общее достаточное условие (см. § 15.7) повышает эффективность метода динамического программирования.

15.9. ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ

15.1. Среди N внешне одинаковых шаров один несколько легче остальных. Требуется указать стратегию для нахождения меньшего по весу шара с помощью минимального числа взвешиваний на весах с рычагами равной длины. Обозначив через/г оптимальное количество (минимум) взвешиваний, покажите, используя принцип оптимальности, что

~ /1/ = 1 + min max [f., / 2у

Найдите

15.2. Требуется выбрать четыре неотрицательные величины х . . ., х с тем, чтобы до-

ставить максимум функционалу f ~ й Сумма величин Х{ ограничена хс= 20. Найдите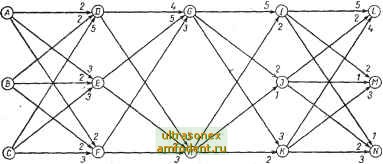

Рис. 15.7. Схема направлений перелетов между городами с промежуточными посадками (цифра над каждой стрелкой указывает стоимость

перелета)

закон выбора в зависимости от а, считая, что а!> 0. Сделайте это сначала с помошью обычных методов, а затем на основе принципа оптимальности.

15.3. Предположим, нам необходимо выбрать наиболее экономичный маршрут перелета из одного города в другой с тремя промежуточными посадками. В одном конечном пункте можно использовать аэровокзалы Л, В или С, а в другом - L, М или N. Кроме того, в качестве пунктов для первой посадки можно выбрать города D, Е или F; пункты С или И могут служить для второй промежуточной посадки, а J, J, или К являются возможными пунктами третьей промежуточной посадки. Стоимость перелета из каждого города в следующий указана на рис. 15.7.

Найдите наиболее экономичный маршрут и его стоимость с помощью:

а) обратного динамического программирования. Сформулируйте принцип оптимальности для этого случая;

б) прямого динамического программирования. Сформулируйте принцип оптимальности и для этого случая;

в) непосредственного перебора всех возможных вариантов.

15.4. Для оптимального по быстродействию управления объектом вида х, = Хо х = и при I и (О I 1 покажите, что:

а) минимальное время f (х), необходимое для перехода из точки jc в начало координат, определяется формулой

/* (JC) =

2x1,

% > g- 2 I 2 I

- 2+у-4x4-2x1 ; - х,<:-- xlxoj;

I 2 I, X, = -g- 2 I % I ;

б) /* (x) удовлетворяет уравнению Беллмана, и dt*/dx определяет сопряженные переменные, если соответствующие пределы существуют (заметим, что dt*/dt= 0).