Величину д= -=-2--скоростной напор можно выразить лишь функцией

времени q (t).

Задача сводится к нахождению а как функции времени с учетом ограничения а ащах с тем, чтобы ракета имела возможность пройти из начальной точки (х у,) в конечную точку (х2, У2) за минимальное время.

Приняв X, = х; Х2 = х\ Xg = у; х= у; и = сд (f) а/т я = т/с система уравнений будет иметь вид

. .

X, - Xg, Xg - ч > Xg - Х4, Х4 - и;

ее можно представить в форме х= Ах-{- g{u), где

0 10 0-

0 0 0 0

0 0 0 1

.0 0 0 0

Ограничение на функцию и сводится теперь к м мощью принципа максимума находим

- О

Kq (t), где К2 = CiKmax/m. с по-

Я = 11)1X2+1)33X4 - 11)2

-bll)4M- 1.

Для максимизации Н рассмотрим два случая:

1) I и К Kq (О - Здесь Н можно максимизировать, взяв ее производную по м и приравняв ее нулю:

=-2il)2.Ki11)4=0.

Это дает

q(t)

211)21

Для нахождения и Ф4 рассмотрим сопряженную систему, откуда можно определить, что 11)2 и 11)4 будут иметь вид 11)2 = С2 (2 - -); Ф4 = Сз (2 - 0. так как (к) (2) = О ), где С2 и сз - постоянные. Поэтому

= -шг - 2 < ж < =

Таким образом, для данного случая функция управления и должна быть пропорциональна д, а это значит, что а = ти/(с,д) должна быть постоянной;

2) 1 м I = K2q (О = max (или а шах). Это действительно так, если Cs/( = К1К2 = = ос,лах, и вместо приведенного выше выражения имеем

и* = sign

Кд (t) или а* = sign

Сшах-

Во всех примерах, рассмотренных в данном параграфе, необходимо учитывать тот факт, что принцип максимума обеспечивает лишь необходимое, но недостаточное условие оптимальности. Таким образом, согласно материалам гл. 13, мы нашли лишь локальный минимум. Во многих случаях принцип максимума обеспечивает также и достаточное условие оптимальности.

1) Поскольку Х2 = X и Х4 = не фиксированы в момент времени t = tz, то из формулировки 3) теоремы 14.3 следует, что 12 (4) = t (У = 0.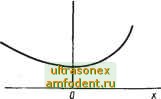

14.4. ПРИНЦИП МАКСИМУМА КАК ДОСТАТОЧНОЕ УСЛОВИЕ ОПТИМАЛЬНОСТИ

Часто говорят, что принцип максимума обеспечивает ряд сильных необходимых условий, т. е. условий, которые в некотором смысле близки к до- статочным. Для линейного объекта можно показать, что принцип максимума является достаточным условием оптимальности.

Ниже приводится достаточно общая формулировка теоремы о достаточных условиях принципа максимума в случае управления линейным объектом ).

Теорема 14.4. Пусть для системы f(>)

x==A{t)x + g(u,t) (14.41)

показатель качества определяется вспомогательным дифференциальным уравнением

Xo = h{x,t) + go{u,t), (14.42)

где А, fo, go и - функции, непрерывные по Рис. 14.5. Выпуклая функция всем аргументам, а /д также однозначная вы- f W

пуклая функция ) от х для каждого фиксированного значения t. Цель управления совпадает с изложенным в п. 2 § 14.3. Если найдено управление и* (t), удовлетворяющее принципу максимума и условиям задачи, то оно является оптимальным.

При этом видно, что функция и (t), найденная для каждого из примеров в § 14.3, действительно определяет оптимальное управление.

14.5. СХЕМА ДОКАЗАТЕЛЬСТВА ПРИНЦИПА МАКСИМУМА

В данном параграфе будет показано, как можно использовать понятие достижимого выпуклого множества, введенное Беллманом и Ла-Саллем для построения доказательства принципа максимума для линейных систем. Затем будут указаны шаги, необходимые для распространения этого доказательства на общий случай [69].

1. Доказательство принципа максимума для класса линейных

систем

Рассмотрим линейную задачу, описываемую расширенным матричньш уравнением

x = Ait)x+g{u,t), (14.43)

где управление и входит нелинейно. Как и раньше, примем и,- 1.

Без потери общности, в уравнении (14.43) можно принять, что в результате переноса координат вьшолняется условие х {tj} = 0; таким образом, начальная точка расширенной системы совпадает с началом координат пространства ё..

Пусть задача управления ставится так же, как и в п. 2 § 14.3, за исключением того, что в момент времени желательно привести систему в состояние, где Xi = Si при i == 1, . . . m, и при этом минимизировать координату

1) Доказательство см., например, в работе [119].

) Функция f(x) называется вьшуклой, если для двух любых точек х- х, при всех значениях О а 1 имеем f (ах -Ь (1 - а) х,) а/ (Х]) + (1 -) f (х,). Вьшуклая функция одной переменной / (х) показана на рис. 14.5.

Для упрощения опустим обозначение штриха, указывающее на расширенные векторы. Таким образом, уравнение (14.43) принимает вид

x = A(t)x + g{u, t). (14.44)

При этом имеется в виду, что л: и g- представляют собой (п + 1)-мерные векторы соответственно с составляющими Xq, . ., х, я g, . . ., g , а А обозначает матрицу размерности (п + 1)Х(п+ 1).

Для построения доказательства полезно мысленно представлять себе какую-либо задачу оптимизации в трехмерном расширенном пространстве состояний с координатами Xq, х х- Допустим, требуется обеспечить управление линейной системой третьего порядка вида (14.44), которое переводит ее из состояния х (t,) = О в положение х, (t) = в момент времени t = t, и при этом достигается минимум величины Хо {t. В момент времени координата 2 остается свободной.

Прежде чем приступить к доказательству, примем, как и раньше, что достижимое множество (3 {t представляет собой множество всех точек в +1, достижимых системой (14.44) при выборе и (t) из допустимого множества Q, т. е.

(14.45)1)

Так как g (и, t) не обязательно равно В (t) и (t), то не ясно, является ли теперь множество С (2) выпуклым.

Важным при доказательстве принципа максимума является следующий результат [69].

Лемма 14.1. Если в уравнении (14.44) А {t) кусочно-непрерывна по ty а g (и, f) непрерывна по й и кусочно-непрерывна по t, то множество G {t} является выпуклым.

Зная, что G (tz) выпукло, можно повторить рассуждения, которые привели к результатам для случая задач оптимального быстродействия, при условии, что будут внесены изменения, обусловленные более сложной структурой множества конечных состояний. Следует, однако, отметить, что в лемме 14.1 ничего не говорится о замкнутости G (t)-

Для задач, оптимальных по быстродействию, множество конечных состояний совпадает с точкой л:2- Если определен момент, когда замкнутое и выпуклое множество G (t) в первый раз касается х, то задача решена; из рассмотрения геометрии задачи можно вывести некоторые необходимые условия существования оптимального по быстродействию управления.

В более общем случае, когда G (t) не обязательно замкнуто, нельзя говорить о том, что G (tz) касается какой-то точки ). Однако можно говорить о точках, которые принадлежат или не принадлежат множеству G (g)-

Предположим, что оптимальное управление и* (f) найдено. Пусть соответствующая оптимальная траектория имеет вид х [и* (t), t]. По определению, вектор X [и* (t), t] принадлежит множеству G (t)-

Лемма 14.2. (Принцип оптимального движения) ). Для каждого t из интервала [t, t] х (и*, t) представляет собой граничную точку множества Git).

1) В отличие от § 14.1, где G (t) определялось при х (t ~ О, здесь G {t определяется при х (i) = 0. Результат будет тот же, поскольку всегда можно считать, что х {t ф О п X (У = 0.

) Если А (t) непрерьшна ио t, а g (и, t) непрерьшна по иш t, то тогда при \ис\ 1 множество С (4) является и замкнутым, и вьшуклым [149]. ) Доказательство см., например, в работе [52].