/ (х) или [x (t)}

Re N (х)

Im N (х)

О для кА

для х:

О для X 4АВ

для хЛ

О для Х: Л -[-В

л + в

\х-2Л

для хЛ+В

О для Х:Л -1-В

4Ы (Л + В -X)

для хЛ -j-B

О для хЛ +В

l-Ni

хЛ + В/

\х-2Л/

для Л+ВхС

С-2л;

\л + в,

для х:

О для хЛ + В

4Ы (Л+В-х) лха

для Л +B:s;xC 4М(Л--В-С) лх2 длял; с

О для х Л -1-В

X /

В-Ь Л\

X / для хЛ-1-В

О для х<Л --В 4ЛС лх2

для хЛ -j-B

* Таблицы 6.1 и 6.2 заимствованы из статьи К. М а g п и s а. Uber ein Verfahren zur Untersuchung nichtlinearer Schwingungs - und Regelungs - Systeme. VDI - Forschungsheft, 19SS.

** Здесь и везде далее в таблице под k понимается соответствующий коэффициент нарслоиа прямой к нелинейности.

6.3. ЭКВИВАЛЕНТНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДВУЗНАЧНЫХ НЕЛИНЕЙНОСТЕЙ

До сих пор рассматривались эквивалентные коэффициенты усиления лишь для однозначных нелинейностей. Под однозначным безынерционным нелинейным элементом понимается такой элемент, реакция которого на входной сигнал мгновенна и соответствует его статической характеристике показанной на рис. 6.8, а. Достаточно часто элементы, встречающиеся в системах управления, являются двузначными нелинейными инерционными

Выход

выход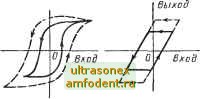

Вход

о) б) В)

Рис. 6.8. Характеристики нелинейностей:

Выход

а Вход -А

а - однозначная (с нулевой памятью); б - двузначная {типа гистерезис ); в - двузначная (типа люфт ); г - двузначная (релейная с гистерезисом)

элементами. Следовательно, связь между входом и выходом не определяется однозначно статической характеристикой нелинейности, а зависит от начального состояния элемента и предыстории входного сигнала. Примерами такого типа нелинейностей являются элементы типа гистерезис , люфт -и реле с гистерезисом. Они показаны на рис. 6.8, б, 6.8, в и 6.8, г для одного периода входного сигнала заданной амплитуды. Для больших амплитуд, эти характеристики принимают вид, показанный на рисунке пунктиром. Для релейного элемента с гистерезисом оказывается, что его характеристика не меняется при увеличении входного сигнала.

Поскольку выходной сигнал двузначной нелинейности зависит от предыстории входного сигнала, то соотношение между входом и выходом для такого элемента математически можно описать только посредством функционала, который можно назвать функцией от функции, когда входной функции

ставится в соответствие выходная величина. Если входную и выходную функции времени обозначить через X (t) и у (t), то функционал, их связывающий, запишется так:

y{t) = [x{t)]. (6.32)

В дальнейшем, используя структурную схему (рис. 6.9), будем помнить, что соотношение между выходом и входом задается соотношением (6.32).

Пример 6.4. Рассмотрим релейный элемент с гистерезисом (см. рис. 6.8, г). При синусоидальном входном сигнале выходной представляет последовательность прямоугольных импульсов, не зависящую от амплитуды входного сигнала, если она превышает половину ширины петли гистерезиса (величина а на рис. 6.8, г и рис. 6.10). Поскольку частота повторения прямоугольных импульсов равна частоте входного сигнала, то прямоугольный импульс пересекает нулевой уровень с запаздыванием по отношению ко входу. Это означает, что эквивалентная передаточная функция характеризуется, фазовьм сдвигом, а в частности, фазовым запаздыванием.

Если быть более точным, то при входной амплитуде, равной а, первая гармоника выходного сигнала будет иметь отставание в 90°. Однако это отставание будет уменьшаться с ростом амплитуды а входного сигнала, и в пределе оно стремится к нулю. Кроме этого, эквивалентная

Рис. 6.9. Изображение на структурных схемах нелинейного элемента, представляющего собой функционал

амплитудная характеристика рассматриваемого нелинейного элемента во многом подобна идеальной релейной характеристике, в которую переходит релейная характеристика с гистерезисом при стремлении величины а к нулю.

Для ТОГО чтобы получить аналитическое выражение для эквивалентной передаточной функции, будем считать, что входной сигнал синусоидален, и, разложив в ряд Фурье выходной сигнал, найдем члены, зависящие лишь от первой гармоники. Проделаем это на конкретном примере.

Пример 6.5. Предположим, что начальное значение выходной координаты нелинейной характеристики (см. рис. 6.8, г и рис. 6.10) равно -А, тогда при

входном сигнале е sin mt получим для одного периода колебаний 0:cu/:2jt следующее выражение для сигнала и (/):

-А, п -j- arcsin < со/ < arcsin-

+Л, arcsin < со/ < л + arcsin

Разлагая и (t) в ряд Фурье

U (/) = 1 sin со/ -j- Pi cos со/ -----,

получим *

Рис. 6.10. Вид сигнала на выходе нелинейного элемента, представляющего собой реле с гистерезисом (при входном синусоидальном сигнале)

о, =

arcsin

-Я-Ьа resin -

fft-l-arcsin

Sin atd (mt) -j- ( sin mtd (cot)

fft+a resin

cosco/d(cu/) -j-

cos cotd (cot)

-п-1-а resin - e

aresin -

Эти соотношения верны, если е> а; тогда амплитуда первой гармоники выходного сигнала равна ♦

а фаза определяется соотношением

arctg - = arctg -

arcsin -

отсюда следует, что эквивалентная передаточная функция имеет вид

-/aresin -

Подобное явление уменьшения фазового сдвига, когда амплитуда возрастает, встречается довольно часто. Читатель может проверить такое

* Коэффициенты 1 и Pi в отечественной литературе принято называть первыми коэффициентами гармонической линеаризации {Прим. ред.).