Оказывается возможным анализировать орбитальную устойчивость и по линеаризованным уравнениям. Поскольку изложение этих идей требует дополнительных определений, то мы вернемся к ним в гл. П.

Можно лишь отметить, что классическое определение устойчивости предельного цикла (см. гл. 4) соответствует орбитальной асимптотической устойчивости. В следующем параграфе излагаются некоторые полезные результаты исследования орбитальной асимптотической устойчивости предельных циклов в системах второго порядка.

5.8. ПРЕДЕЛЬНЫЕ ЦИКЛЫ В СИСТЕМАХ ВТОРОГО ПОРЯДКА И ИХ ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ

Рассмотрим четыре важнейших теоремы о существовании предельных циклов.

Первая теорема принадлежит А. Пуанкаре и связывает факт существо-, вания предельного цикла с типом особых точек, расположенных в области фазового пространства, ограниченной кривой предельного цикла.

Пусть число N обозначает количество особых точек типа узел , центр и фокус внутри области, ограниченной траекторией предельного цикла, а S - число седловых точек в той же области. В этом случае справедлива следующая теорема.

Теорема 5.3. (А. Пуанкаре). Если в системе второго порядка существует предельный цикл, то N - 5 = 1*. Читатель сам может без труда убедиться в справедливости этого утверждения, проанализировав ряд фазовых портретов. Полное доказательство теоремы можно найти в книге Е. А. Коддингтона и Н. Левинсона [351.

Следующая теорема принадлежит И. Бендиксону [16]; ее иногда называют первой теоремой Бендиксона, и в ней формулируется достаточное условие отсутствия предельного цикла.

Теорема 5.4. (И. Бендиксон). Если система второго порядка описывается уравнениями

Xi = fl (xi, Xg); Xg = /2 (-i.

и при этом существуют частные производные функций (xi, х) и /2 (х, Ха) по каждой из переменных, то предельный цикл не существует в той области фазовой плоскости, где -)- ~- не стремится к нулю и не изме-няет знака.

Доказательство. Вдоль всякой траектории на фазовой плоскости справедливо соотношение

dXi h

(5.63)

которое можно переписать в виде

/2 dxi - /1 dxa = 0. (5.64)

В частности, условия (5.63) и (5.64) выполняются и для предельного цикла.

* Числа N к S можно определить по отношению к области, ограниченной произвольной замкнутой кривой, а не только траекторией предельного цикла. Поэтому разность N - S часто называют индексом Пуанкаре.

Допустим, что предельный цикл существует, и проинтегрируем выражение (5.64) по замкнутому контуру:

(fl - /2 dxi) = О, (5.65>

♦

где G - траектория предельного цикла.

Воспользуемся теоремой Стокса *, которая связывает интеграл по замкнутому контуру с интегралом по площади, ограниченной этим контуром. Тогда можно записать

ф (fl dx, ~ hdxi) J j (- + dx (5.66).

где интеграл в правой части берется по площади, ограниченной траекторией предельного цикла.

Учитывая (5.65), правая часть выражения (5.66) должна стремиться к нулю, но этого не может быть, поскольку подынтегральное выражение

ж ° условиям теоремы не стремится к нулю и не меняет знака.

Это противоречит предположению о существовании предельного цикла, что и доказывает теорему.

Следующая теорема также принадлежит Бендиксону; ее иногда называют второй теоремой Бендиксона.

Теорема 5.5. (И. Бендиксон). Если траектория автономной системы второго порядка все время остается внутри ограниченной области <01 и при этом не стремится к положению равновесия, то такая траектория либо представляет кривую предельного цикла, которая обладает свойством орбитальной асимптотической устойчивости, либо стремится к предельному циклу с тем же свойством.

Теорема достаточно очевидна, но доказательство несколько сложно и поэтому нами опущено **.

Обратимся к примеру.

Пример 5.21. Для лампового генератора, изображенного на рис. 5.6, а, выполняется следующее условие;

Пусть

of(M, (5.68),

где бо - постоянная величина;

f (1) - нелинейная характеристика, показанная на рис. 5.6, б При этих условиях соотношение (5.67) запишется в виде

* Эту теорему иногда связывают и с именем Гаусса. ** См. [16J.

*** Отметим, что / (0) 0.

(5.70)

Проделаем теперь следующее:

1) проанализируем существование и устойчивость особых точек;

2) определим то значение усиления к, которое является необходимым условием для существования предельного цикла;

3) найдем необходимое и достаточное условие, накладываемое на величину к, которое обеспечивает предельный цикл.

Структурная схема для этой системы показана на рис. 5.6, е. Анализируя работу генератора, можно предположить, что начало координат Xi = х = О является положением равно-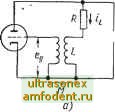

В) г)

Рис. 5.6. Ламповый генератор:

+7 X,

а - принципиальная схема лампового генератора; б Mi е

лампы / (д;,) =--е в зависимости от х,= -2-; е-структурная схе-

JA Lc 0

ма лампового генератора, изображенного на рис. 5.6, а; г

Г Ixi) = в функции от х,

характеристика

. зависимость

весия. Ведь действительно ввиду дифференцирующих свойств линейной части постоянная составляющая тока (ток покоя) не вызывает увеличения постоянной составляющей сигнала на выходе; но в силу положительной обратной связи можно ожидать, что начало координат неустойчиво. Из уравнения (5.69) нетрудно получить следующую систему:

-2- . - (5.71)

Заметим, что

Ч = х.2\ Х2 = -2oCOoX2 - coqxi + Ир f (xi).

df Ы

(5.72) (5.73)

Зависимость f (x) показана на рис. 5.6, г. Из рис. 5.6, б или 5.6, г следует, что

с учетом выражений (5.72) и (5.73) уравнения (5.71) примут вид

Хх = х; 2 = - (2о - / (х{)) ых - cogxi (5.75)