при 9 = 0 окружность симметрична относительно действительной оси и

проходит через точки--- и--.

6. Выполнение требования теоремы 10.4 об устойчивости линейного элемента, охваченного отрицательной обратной связью с коэффициентом а, можно проверить с помощью частотного критерия устойчивости. Если G (s) представляет рациональную функцию комплексной переменной s и число полюсов этой функции в области Re s О обозначить через г, то требование устойчивости линейной части системы выполняется, если частотный годограф функции G (/со) при -оо со оо и при условии, что каждый полюс, расположенный на оси Re s = О, обходится вдоль окружности бесконечно малого радиуса, расположенной слева от полюса, совершает вокруг точки

-- ровно г оборотов против часовой стрелки *. Для случая 9 = 0 указанный критерий можно объединить с условием (10.36). Вывод соотношения мы предлагаем проделать читателю самостоятельно (упражнение 10.18), однако окончательный результат сформулируем в виде следствия.

Следствие 10.1. Пусть G (s) представляет рациональную функцию переменной s, причем порядок знаменателя выше порядка числителя, а число полюсов в области Re s О обозначим через г. Пусть и (t) = [е (t), t], и, следовательно, рассматривается общий вид нестационарной нелинейной характеристики. Для того чтобы основная система (10.1) с обратной связью обладала абсолютно асимптотически устойчивыми управлением и выходным

сигналом для (и/е) G Ы, Ь] при a<i b и > -j-. достаточно, чтобы годограф G (/со) при -оо со оо, когда обход каждого полюса, расположенного на мнимой оси Re s = О, совершается по полуокружности бесконечно малого радиуса слева от полюса, располагался вне окружности, проходящей

через точки---и-- с центром ---т-и охватывал эту окруж-

Ct и 2i

ность г раз при движении против часовой стрелки.

Для доказательства теоремы 10.4 рассмотрим преобразование (10.29), связанное со сдвигом полюсов, из которого следует, что если (и/ё) G \а, Ь], то (Мд/е) G [0,6 - а]. Кроме того, линейная часть преобразованной системы, определяемая по соотношениям (10.30) и (10.31), предполагается устойчивой **. Следовательно, условие теоремы 10.1 выполняется для преобразованной системы, и условие Попова (10.19) можно переписать в виде

Re[(1 -Ь/со9) G (/ )] -f 8>0,

где G(j (/со) определяется в соответствии с выражением (10.30); б - бесконечно малая постоянная (с какой целью она вводится?).

Отметим, что, согласно выражению (10.30), сдвиг полюсов (10.29) определяет билинейное преобразование комплексной переменной G (/со) в G (/со). Такое билинейное преобразование переводит окружности и прямые линии либо в окружности, либо в прямые. Так, например, прямая Попова (рис.

10.4а) переходит в окружность на рис. 10.10. Более того, при ~ ~у

область справа от прямой Попова переходит в область вне критического

* Читатель может сам убедиться, что согласно обобщенному круговому критерию (10.36) охват точки - 1/а равносилен охвату отрезка [-l/a, -l/b] при 1/и> 1/Ь или интервалов [-оо, -1/Ь] и [-1/а, со] при ]/а< 1/Ь.

** Это требование будет ослаблено в теореме 10.6.

круга на плоскости G (/со) (см. рис. 10.10) . Последняя точно соответствует условию (10.36). Таким образом, если выполняется условие (10.36), то для преобразованной системы существуют асимптотически устойчивое управление и асимптотически устойчивый выходной сигнал, т. е. выполняются неравенства

1 со

ul (t) dt <оо; I (О dt <оо

для произвольных начальных условий. Отсюда, пользуясь условием (10.29) для исходной системы, получим

j {t)dt<oo

для произвольных начальных условий. Следовательно, для исходной системы также существуют асимптотическое устойчивое управление и асимптотически устойчивый выходной сигнал. Доказательство теоремы на этом заканчивается.

В отличие от приема, который использовался при построении прямой Попова (раздел 10.3), в данном случае нет большого смысла в преобразовании критических окружностей из плоскости О (/со) в плоскость G* (/со), поскольку при этом получается семейство кривых (отличных от окружностей), вид которых зависит как от q, так и от со (обратите, однако, внимание на упражнение 10.17). Кстати, из теоремы 10.4 следует интересное свойство.

Если провести касательную к критической окружности в точке--,

то ее наклон будет определяться как. Это показано на рис. 10.10. Сравнивая рис. 10.10 с рис. 10.4 а, нетрудно заметить, что касательная к критической окружности имеет тот же наклон, что и прямая Попова, если а = 0. Действительно, если Ь = К и 0а-<-6, касательная просто совпадает с прямой Попова, изображенной на рис. 10.4а. В разделе 10.3 было показано, что эту прямую можно перевести в линию на плоскости G* (/со), не зависящую от изменения частоты (см. рис. 10.5). Таким образом, если G* (/со) лежит справа от прямой Попова на рис. 10.5, то это означает, что G (/со) лежит вне критического круга на рис. 10.10. При этом лишь должно соблюдаться условие теоремы 10.4 об устойчивости линейной части системы, охваченной обратной связью. Этот вывод сформулируем в виде теоремы.

Теорема 10.5. Рассмотрим основную систему (10.1). Пусть ее линейная часть, охваченная отрицательной обратной связью с коэффициентом а > О, устойчива. Для того чтобы в исходной системе с обратной связью управление и выходной сигнал были абсолютно асимптотически устойчивы в секторе (и/е) G la. К], достаточно, чтобы нашлось такое действительное число q, при котором для всех со О вьшолняется условие Попова (1.0.9) при тех же ограничениях на д иК, что и в теореме 10.1.

1 При 1/о;< 1/Ь область справа от прямой Попова переходит в область критического круга.

Неравенство Минковского (см. приложение П1) определяет, что

< CD.

Угол между касательной и вертикалью в точке -1/Ь равен arctgHco.

Отметим, что теорема 10.5 позволяет проводить графический анализ на плоскости G* (/со) с помощью выражения (10.22). Ее преимущества наиболее полно проявляются при анализе систем с неустойчивой и находящейся на границе устойчивости линейной частью. Теорема позволяет применить условия Попова непосредственно к исходной системе, не подвергая ее никаким преобразованиям (см. пример 10.6) при условии, что линейный элемент, охваченный отрицательной обратной связью с коэффициентом а, устойчив.

Обратимся вновь к рис. 10.10. При этом будем помнить, что в теореме 10.4 используется понятие критической окружности, а в теореме 10.5 - понятие прямой Попова. Из рис. 10.10 следует, что хотя теорему 10.5 применять и проще, но ее условия ослаблены и являются достаточными по отношению

к условиям теоремы 10.4. Однако, если рассмотреть такие важные для практики случаи, когда в состав структурной схемы входит интегратор или генератор свободных колебаний (для которых требуемое для экспоненциальной устойчивости значение а мало) *, то можно заметить, что прямая Попова лишь незначительно сдвинута вправо от критической окружности-при любой частоте, и, следовательно, для таких передаточных функций теорема 10.5 справедлива.

С помощью теоремы 10.3 теорему 10.5 можно использовать чтобы определить, существуют ли асимптотически устойчивое управление и асимптотически устойчивый выходной сигнал с порядком сходимости а ф 0.

Пример 10.7. Рассмотрим ту же систему, что и в примере 10.6. Ранее было показано, что линейная часть, охваченная отрицательной обратной связью с коэффициентом а, где 12 <; а <; 42, устойчива. Для применимости теоремы 10.5 следует рассматривать лишь нелинейные элементы, для которых (ule) £ [а. К).

У функции G (s) вида (10.32) модифицированная частотная характеристика G* (/ш) = = Re G (/со) /ш Im G (/со) показана на рис. 10.11. Из рисунка следует, что прямую Попова можно провести через точку чуть левее Re G* (/со) =-Va- Кроме того, ее можно провести вертикально, т, е. считая 9=0, что соответствует самому общему случаю нелинейной характеристики. Итак, К = 12 - е, где е > О, следовательно, сектор Попова определяется соотношением (ule) g [а, 12 - е], где 12<о;<42. Однако при о;> 12 сектора не существует, и теорема 10.5 не даст нам никакой информации.

Пример 10.8. Вновь обратимся к системе, рассмотренной в примерах 10.6 и 10.7, и исследуем преобразованную передаточную функцию (10.33) при а = 12 **, записанную в виде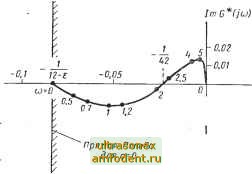

- - 0,01

Рис. 10.11. Модифицированный частотный годограф передаточной функции G (s) =

= (s-l)(s + 3)(s+4) для примера 10.7

Ga is) =

s ( + 6s + 5)

s(s+ 1) (s+ 5)

eao{t) = -j- (l2xio - 4x20 - Зхзо) + (бхю - 6X20 - 4xse) e +

(10.37)

* Если линейный элемент приобретает свойство экспоненциальной устойчивости при любом сколь угодно малом коэффициенте обратной связи, то говорят, что такой элемент предельно устойчив [1].

** Это равносильно передаточной функции (10.35) при е = 0.