Входной сигнал г (t) и реакция на начальные условия линейной части исходной системы согласно выражению (10.29) должны быть заменены на Га (О и ео (t), определяемые через преобразование Лапласа следующим образом:

[Гаit) + (01 = T+W + -

Вывод соотношений (10.30) и (10.31) мы предлагаем читателю сделать самостоятельно (см. упражнение 10.2). Из выражений (10.30) и (10.31) видно, что преобразование (10.29) приводит к изменению корней х ар актер истиче-

t/ = f {e)=Uae

t) e(t)

Un(t)

Ga(p)=

G(p)

UGlp)

Рис, 10.9. Преобразование, связанное со сдвигом полюсов:

а - влияние преобразования на изменение характеристики нелинейного ,

элемента; б - исходная система, где о it) - реакция линейного элемента иа начальное условие, а г (f)-входной сигнал; в-преобразованная система в результате замены (t) = и (t) - ае (t)

ского уравнения системы; поэтому указанное преобразование и называется сдвигом полюсов. Данный прием удобно использовать для анализа систем, линейная часть которых либо неустойчива, либо находится на границе устойчивости. Он же позволяет дать доказательство основной теоремы 10.1 для случая -оо <; 90 (см. приложение III).

Пример 10.6. Рассмотрим линейный элемент, передаточная функция которого и реакция на начальные условия задаются в виде

G(s) =

(s- 1) (s+ 3) (s+ 4)

(10.32)

где (Xie, Xjo, x) - совокупность начальных условий для некоторого набора переменных состояния. Очевидно, что такой элемент неустойчив. Однако линейную часть можно сделать устойчивой, если охватить ее отрицательной обратной связью с коэффициентом а. Для преобразованной линейной части в соответствии с выражениями (10.30) и (10.31) получим

[ga(0]= G (S)=

(s+3) (s-

s (s? + 6s + s) -f a -- 12

4) Xio+ (s-1) (s+ 4)X20+ (s-1) (s-f 3) Х30 s (s2 + 6s + 5) + a - 12

(10.33)

Методом корневого годографа или с помощью любого другого метода можно показать, что преобразованный линейный элемент устойчив, если

12<а<42.

(10.34)

Для этих значений я из выражений (10.33) следует, что как (t), так и ео (О ограничены убывающей экспонентой, т. е. существуют постоянные Ki, К21 О такие, что

1 & (О К Ki ехр (-EiO и I е о (О 1 < Кг ехр (si).

Таким образом, преобразованный линейный элемент удовлетворяет условию (10.9) при ct = О и по определению 10.3 является устойчивым (покажите это). Величину а можно выбр ть равной й = 12 -f- е, где О < е < 15, и воспользоваться теоремой 10.1 для передаточной функции

Теперь можно определить допустимый сектор Попова для нелинейного элемента. Пусть этот сектор для преобразованной системы определяется как (uJe) [О, KaV, в этом случае из выражения (10.29) следует, что сектор Попова исходной системы будет (и/е) £ [а. Ко -г й]. В частности, для данного примера можно показать, что если характеристика нелинейного элемента стационарна и однозначна либо относится к виду характеристик с активным гистерезисом, то найдется такое 9>0, которое удовлетворяет условию (10.19), если (uJe) [О, 30 -2е] и 0<Е:15 (см. упражнение 10.4). Поскольку а= 12-- е, то из выражения (10.29) следует, что сектор Попова исходной системы, для которого гарантируется существование асимптотически устойчивого выходного сигнала, определяется условием (и/е) [12-i-e, 42 - е], где О < е 15. Сравнив это условие с ограничением (10.34), видим, что в данном случае сектор Попова совпадает с углом Гурвица. Это означает: гипотеза Айзермана выполняется.

2. Обобщенный круговой критерий *

До сих пор мы шли по пути преобразования передаточной функции исходной системы к такому виду, чтобы выполнялись условия теоремы 10.1. Теперь мы попытаемся видоизменить условие Попова (10.19) так, чтобы оказалось возможным анализировать систему с первоначальной линейной частью. Этот путь приводит нас к чрезвычайно полезному круговому критерию, который мы и сформулируем в качестве теоремы.

Теорема 10.4 Рассмотрим основную систему с обратной связью (10.1). Допустим, линейный элемент, охваченный отрицательной обратной связью с коэффициентом а, устойчив. Для того чтобы для исходной системы с обратной связью существовали абсолютно асимптотически устойчивое управление и выходной сигнал при (и/ё) 6 [а, Ь], если а <С. Ь, достаточно существование такого действительного числа д, что для всех ю О выполнялись условия

G0 ) +

6 + а - /СО)? (6 - а)

G(/o)) +

b+a-

- jag (b - a)

>

b - a

<

(10.36)

* Круговой критерий был первоначально доказан лишь для случая д= О ([24], [207], [208]). Обобщенный круговой критерий, сформулированный в теореме 10 4, является дальнейшим развитием и справедлив для д фО.

** а и b могут принимать отрицательные значения, и, следовательно, могут выполняться

оба условия: - !> -г- и - < -т- .

где б - произвольно малая величина. Ограничения, которым должны удовлетворять величины д и b - а, зависят от вида нелинейности и остаются теми же, что и в теореме 10.1 для величин q иК соответственно.

Геометрическая интерпретация условия (10.36) состоит в том, что для всех О) О частотный годограф G (/со) должен располагаться вне или внутри круга с центром в точке

в зависимости от, выполнения условия

>

или -<

И пересекать

действительную ось в точках --и --Рис. 10.10 построен для

распространенного условия Пример, соответствующий

приводится в § 10.8.

ImCfju)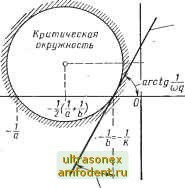

Пряная Попова

ReGljcj)

arctgcjq

Рис. 10.10. Графическая иллюстрация теоремы 10.4 для случая 1/й > 1/Ь, а также теоремы 10.5

наиболее

а b

условию > -

Подведем некоторые итоги:

1. Теорема 10.4 обобщает основную теорему 10.1. Можно показать, что если а О и b К, то условие (10.36) переходит -в условие (10.20) (покажите это) *, которое, в свою очередь, соответствует условию (10.19) в теореме 10.1.

2. Для существования абсолютно асимптотически устойчивых управления и выходного сигнала с коэффициентом затухания а требуется, чтобы, во-первых, линейная часть, охваченная отрицательной обратной связью с коэффициентом а О, обладала степенью устойчивости а и, во-вторых, вместо частотной характеристики G (/со) в условие (10.36) следует подставлять G (/со-а). Это является непосредственным следствием теоремы 10.3.

3. Рис. 10.10 иллюстрирует также связь, которая существует между ограничениями на линейную и нелинейную части системы. Сужая сектор {ule)£ [а, Ь], мы уменьшаем и радиус критических окружностей. Поэтому область допустимых расположений годографа G (/со) расширяется.

4. Если а /I и 6 /I, то мы получим линейную стационарную систему с усилением h. В данном случае критическая окружность вырождается в точку

с координатой --на плоскости G (/со). Это и есть критическая точка при

формулировке частотного критерия устойчивости линейной системы.

5. Критическая окружность, определяемая соотношением (10.36) и показанная на рис. 10.10, является функцией частоты или, точнее, произведения д(д. Несмотря на то, что все окружности проходят через точки -

и-- их центры смещаются вверх с увеличением произведения щ. Лишь

* Графическое подтверждение указанного положения можно получить и при анализе рис. 10.10, если а = О и Ь = К.