при возмущении Дсо (о по начальным условиям (t) и возмущении .r{f)£S2 по входному сигналу г (f) получим относительно возмущений уравнения вида

Де (о = Аео {t) + Ar{f)~\g{t~ т) /д (е (т), Де (т)) dx, (11.60)

/д (е (О, Де (0) = / (е (О + Ае (0) - / {е (0)-

(11.61)

Пусть Дм () = /д (е (f), Де (0) рассматривается ности f при входе е ( и входном возмущении Де ().

Обозначив через Дм () возмущение выходного сигнала нелинейности f, получим, что связь между ними задается кривой на рис. 11.3.

Итак, уравнение (11.60) описывает систему с-нелинейностью /д {e{t), Де (х)), которую относительно возмущений можно рассматривать как нестационарную нелинейность /д (Де (f), f). Таким образом, круговой критерий, сформулированный в теореме 10,4, можно применить при <7 = О к системе (11.60).

Пусть

как выход нелиней-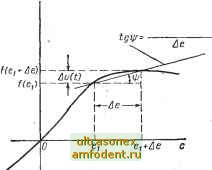

[К К], (11.62)

Рис. 11.3. Зависимость между вариацией Ае около значения е = функции ы = / (е)

тогда по теореме 10.4 система (11.60) имеет асимптотически устойчивые управляющий и выходной сигналы, если:

1) выход системы с передаточной функцией G (s)/[1 + kG {s) \ устойчив;

2) годограф G (/со) лежит вне (внутри) круга с центром на действительной оси, проходящего через точки \lky и 1/2, если (l/A) > {llk. [если (l/i) <; (1/2) ] Переходя к параметрам исходной нелинейности, соотношения (11.62) можно записать

f(e{t)+e{,t))~fie{t))

Ae(t)

(11.63)

(11.64)

для любых е (О и Де (О или

f(ea)~f(eb)

Ва - еь

для любых ва И еь-

Если / (е) - непрерывно дифференцируемая функция переменной е, то необходимым и достаточным условием выполнения неравенства (11.64) является

(11.65)

для всех е.

Заметим, что если г () = О и Дг ( ~ О, то для устойчивости процесса еще требуется, чтобы реакция на любое возмущение начальных условий была достаточно малой. Это и есть исходная задача Попова, и теорему 10.4 можно непосредственно использовать для случая, когда г {{) = 0.

Пусть (ы/е) € IKi, KV, или

(0 e(t)

-.Ко,-

(11.66)

Очевидно, что дли любой функции / (е) диапазон изменения тангенса угла наклона /(е) должен включать диапазон изменения f(e)le, тогда имеем

1 КгК,

(11.67)

ImGfjcj)

Это свойство иллюстрируется с помощью круговой диаграммы (рис. 11.4). В случае, когда г (f) = О, достаточное условие асимптотической устойчивости выходного сигнала заключается в том, что годограф G (/со) не касается малого круга, проходящего через точки - lIKi и l/ZCa- Если

г {t)=hO, для существования асимптотически устойчивого управления для возмущенной системы (11.60) требуется, чтобы годограф G(/(o) не касался большого* круга, проходящего через точки - 1/1 и l/fe. Далее, по лемме 10.1 можно заключить, что Дг/ (/)->0 при / оо.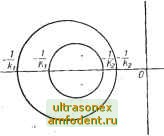

ReC(iu)

Рис. П.4. Круги при -j->->

>->-г-, характеризующие до-

статочные условия устойчивости системы, когда годограф G (/ш) остается не только вне круга, опреде-

3. Нелинейная нестационарная система

Приведенный выше анализ может быть распространен на случай нестационарной нелинейной функции и = f [е, t). Здесь основные уравнения (11.64) и (11:65) преобразуются к следующему виду:

и /(бя, t)-f{eb, t)

ляемого сектором Попова

€ 21. но и вне большого

круга, определяемого соотношением

Ik 2]

Ва - еь

для любых ва, вь И t И

i де

(11.68)

(11.69)

для любых t соответственно. Чтобы обобщить результаты этого параграфа, сформулируем следующую теорему.

Теорема 11.7. Для системы, показанной на рис. 11.1, предположим, что существуют такие две константы! и kz, что условие (11.68) удовлетворяется; тогда для любого ограниченного входного возмущения Дг (/) G =22 и для любых возмущений реакции у (fj на начальные условия возмущение Ау (f) будет стремиться к нулю при t-oo, если:

1) линейная система с передаточной функцией G (s)/[l -+- kG (s)] имеет устойчивый выходной сигнал;

2) годограф G (/со) лежит вне (внутри) круга, проходящего через точки l/k и 1/2. если (l/kj) > (1/2) [если (l/ki) < (1/2) . с центром на отрицательной действительной полуоси.**

* Круги на рис. П.4 показаны для случая Ai> 0. Если Ai<; О и (l/iX (1/2). то годограф G Ош) должен лежать внутри круга с центром на действительной оси и проходящего через точки -V/ki и -l/k (см. теорему 10.4).

** Так как теорема 11.7 была получена непосредственно из теоремы 11.4, то круговой критерий (10.36) при (7=0 применим к обоим случаям (l/fei> 1/2 и l/i<I 1/г).

Данная теорема может быть, например, использована при изучении устойчивости вынужденных колебаний. Предположим, что (t) = Уп {t + + Т) - периодическая установившаяся реакция системы с обратной связью (см. рис. И.1) на некоторое периодическое воздействие. Если условия теоремы 11.7 удовлетворяются, то для любого возмущения начальных условий движение у (fj будет стремиться к Уп (t) при t оо независимо от величины действующего возмущения. Это гарантирует единственность установившейся реакции у (t).

Пример П.2. Рассмотрим систему с обратной связью и с нелинейностью типа ограничения. В § 6.5 с помощью эквивалентной передаточной функции было показано, что когда годограф G (/ш) находится внутри определенной области (см. рис. 6.19), то возможно явление скачкообразного резонанса.- Это значит, что в некоторых случаях реакция на периодический входной сигнал может быть неоднозначной. Читатель может проверить это самостоятельно, применив теорему 11.7. В этом случае достаточным условием отсутствия явления скачкообразного резонанса в такой системе б/дет условие Re G (/ш) > -1 (см. задачу 11.11). Обратимся к рис. 6.19, откуда видно, что полученная граница более точная, чем граница областей существования и отсутствия скачкообразного резонанса, определенная приближенным способом, основанным на методе эквивалентной передаточной функции. Действительно можно показать (см. упражнение 11.16), что для всех безынерционных нелинейностей граница скачкообразного резонанса, определенная методом данного параграфа, всегда будет точнее полученной на основе метода эквивалентной передаточной функции.

Следует быть осторожным в утверждении, что при выполнении условий теоремы 11.7 любое вынужденное решение у (t) = у (t + Т) устойчиво и единственно. При этом не обязательно, чтобы функция у (t) имела тот же период, что и входной сигнал г (t). Например, могут-появляться субгармонические составляющие. Однако Якубовичем [202] и Сандбергом [177] было показано, что при определенных условиях для каждого входного сигнала с периодом Т существует единственный выходной сигнал с тем же периодом. Условия, для которых это справедливо, включают случай системы (см. рис. 11.1) с однозначной стационарной нелинейностью и = f (е), для которой удовлетворяются условия теоремы 11.7. Таким образом, для однозначной нелинейности теорема 11.7 дает не только достаточные условия устойчивости и единственности любого вынужденного решения у (f), но и достаточные .условия отсутствия субгармонических реакций на периодическое возбуждение.

Реакция одноконтурной нелинейной системы с обратной связью на периодическое возбуждение будет рассмотрена в следующем параграфе.

11.6. УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

Покажем, что на основе линеаризации можно проанализировать орбитальную асимптотическую устойчивость или что то же - асимптотическую устойчивость решения с известным периодом. Если на стационарную систему X = f {х, и) действует периодический входной сигнал и (f) с периодом Т, то, выразив входной сигнал как функцию t, уравнение системы можно представить в нестационарном виде

x = f{x,t), (11.70а)

где функция / периодична с периодом Т, т. е.

f{x,t) = f{x,t + T). . (11.706)

Системы (П.70а), где / удовлетворяет условию (11.706), называются периодическими системами. Другой случай периодической системы имеет место, когда периодический выходной сигнал вызывает в системе вынужденные колебания.