пользовать ряд способов [115]. Однако применение этого метода ограничено системами сравнительно небольшого порядка.

Вторую группу численных методов образуют непрямые методы. В них для того, чтобы прийти к обычной нелинейной двухточечной краевой задаче, используются необходимые условия. Путем произвольного выбора, например, трех сопряженных переменных и путем обратного интегрирования получаем оптимальную траекторию, которая, однако, приводит к неверному ряду начальных краевых условий. После этого предпринимается попытка систематически варьировать начальное условие с тем, чтобы решить соответствующую краевую задачу. К сожалению, вследствие того, что нормальная задача оптимального управления вообще исключительно чувствительна к начальному условию, в использовании непрямых методов до сих пор еще не достигнуто успеха.

17.2. ИЗУЧЕНИЕ СТРУКТУРЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

В теории оптимального управления предполагается, что для той или иной задачи показатель качества уже существует. Однако на практике задача бывает сформулирована не четко и проектировщику часто приходится находить такой показатель качества, который, по его мнению, наилучшим Образом отвечает требованиям системы.

Если одного показателя качества достаточно, то следует рассмотреть структуру или схему оптимального управления. Необходимо исследовать такие вопросы, как чувствительность характеристик системы к изменениям параметров этой системы. Там, где это необходимо, можно использовать вычислительную машину.

Часто одного показателя качества недостаточно или его невозможно найти заранее, так как многие соображения, обусловливающие характеристики системы, невозможно в простом виде выразить одним критерием. В этом случае может потребоваться изучение различных соотношений с тем, чтобы определить, может ли приемлемое сочетание критериев послужить мерой качества системы. Здесь снова можно с успехом использовать вычислительную машину.

Существует, конечно, много возможных способов изучения основной структуры задачи оптимального управления; в данном разделе рассмотрим метод, предложенный У. Л. Нельсоном [147].

Пример 17.1. Рассмотрим для простоты случай управления искусственным спутником по углу тангажа. Путем регулирования положения спутника по тангажу желательно эффективно обеспечить прием сигнала наземной станции антенной, установленной на спутнике.

Необходимо прежде всего определить значение понятия эффективно , которое обычно отражает пожелание заказчика.

Во-первых, очевидна необходимость экономного расхода топлива для реактивных двигателей. Однако, как мы выяснили из предыдущих глав, оптимальное по расходу топлива управление без ограничения времени может означать бесконечное время вьшолнения задания. Это нарушает наше понятие слова эффективно . Таким образом, для данной конкретной задачи необходимо согласовать требования минимизации расхода топлива и минимизации времени.

Уравнение движения имеет вид

J-ii) L(t)U. (17.35)

Вводя новые переменные

[4it)e(t); x2(t)~Q(t); u{t)

получим следующую систему

ici-Xzi Xz = u{t); I (if) 11.= (17.36)

Целью управления является перевод спутника из произвольного начального состояния x=Xf, в точку начала координат л: = О за время Т с одновременной минимизацией показателя качества вида

a(T)!rfT. (17.37)

Известно, что на практике значение 6, например 6j, неотличимо от -Ь 2пз1 для любого целого числа п, и потому в данном случае задача управления лишь не намного труднее, чем для управляемого объекта с передаточной функцией 1/s. Однако без потери общности эту задачу можно представить в таком виде, чтобы рассмотреть все возможные начальные состояния:

е (0) = вв + 2пл;; п = О, ±1, ± 2, . ... l

(17.38а)

е (0) = е . 1

где бо и ёо - истинные начальные состояния, которые обеспечивают эффективное управление для перевода системы в конечное состояние 6=6=0. Затем выбирается наилучшее решение.

В свою очередь задачу можно представить в такой форме, чтобы отыскивать оптимальные решения для возможных конечных состояний:

.: е = 2йл;, п = 0, ± 1, ± 2,

1 (17.386)

6 = 0 . .j

при заданных начальных условиях.

При выражении через переменные и из уравнений (17.36) ряд начальных условий, описываемых с помощью соотношений (17.38а), принимает вид

xA0).x + 2kn(), k = 0, ±1, ±2,...j .

Х2 (0) = Хао- )

Теперь решение задачи не вызывает трудностей. В частности, чтобы избежать неединственности вырожденного решения, можно показать, что для каждого начального состояния, если принять

1, >1; .

и(о = ] о. ~i\pAt)i; (17.40)

.-1. гра < - 1.

At)==v---0-2- ; (17.41)

(7-o + 2vTx2o + 4vXio)

v=sigTi(Xi + -Lx2o\X2o\) , (17.42)

то функция оптимального по расходу топлива управления определена (покажите это).

Желаемым решение]! задачи управления пространственньш положением спутника является, конечно, такое решение, которое соответствует эквивалентному начальному состоянию, дающему наименьшее зна,чение расхода топлива.

Для рассматриваемой здесь конкретной задачи основное значение имеют две величины,

а именно: интервал времени управления Т и расход топлива на этом интервале ы (т) dx = /

i . о

Выбрав значение отношения вращающего момента к моменту инерции U/J, равное л/5 рад/сек, и начальное состояние (2; 1), находим, что / й Г с учетом требования минимального расхода топлива изменяются, как показано нарис. 17.2а. Можно привести объяснение представленным здесь кривым. Две ограничивающие линии f = Т н f = \хй \ довольно

очевидны сами по себе. Первая из них представляет собой случай, когда данная продолжительность управления Т равна t*, т. е. минимальному отрезку времени, необходимому для достижения точкой начала координат при переходе от данного начального состояния. Вторая линия обозначает минимально возможную величину расхода топлива при переходе от данного начального состояния в точку началакоординат. Интересной особенностью рис. 17.2а является то, что для конечного состояния (0; 0) кривая минимального расхода топливалищь асимптотически

Начальное состояние (2,1)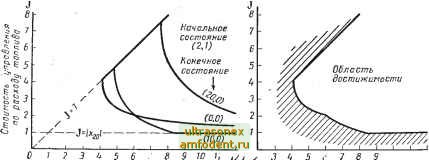

5 Б 7 8 9 10 11 ит 2 3 и 5 6 7 Првдолжительность управления aj б)

10 11 12 Т

Рис. 17.2: а) Кривые зависимости / от Т для системы, рассматриваемой в разделе 17.2; б) Составная кривая, полученная с использованием графика рис. 17.2а, определяющая границу области достижимости (незащтрихованная область): f - стоимость управления по расходу топлива; Т - продолжительность управления

приближается К линии / = [Xaol, тогда как для заданного конечного состояния (10; 0) указанная кривая действительно достигает этой линии (см. рис. 17.3). Из начального состояния (2; 1) можно достигнуть [конечного состояния (О, 0) только с помощью последовательности управления и = -1, О, -Ь1 и невозможно достигнуть точки начала координат при израсходовании минимального количества топлива хв I за какой-то конечный отрезок времени.

Однако для заданного конечного состояния (10; 0) Можно всегда получить условие /= I лао I. если продолжительность управления Т достаточно велика, чтобы позволить состоянию системы переместиться от (2; 1) к линии переключения Pg до включения и= -1. То же рассуждение применимо и к состоянию (20; 0).

Отсюда видно, что для начального состояния (2; 1) нет необходимости рассматривать заданные конечные состояния (-lOifi; 0), п= 1, 2, . . ., так как результирующий расход топлива не может быть меньше, чем для (0; 0). Подобным же образом мы видим, что нет необходимости рассматривать конечные состояния за пределами точки (10; 0).

Взяв те части кривых зависимости f от Т, которые дают минимальное значение f для данного Т, получим составные оптимальные кривые (рис. 17.2, б). Каждая точка на кривых представляет собой отдельную оптимальную конструкцию, отличающуюся от других. Реальная система может дать лишь точки, лежащие в незаштрихованной области на рис. 17.2, б *

Рис. 17.3. Фазовая плоскость, показьшающая конечное состояние (10; 0), которое может быть достигнуто от (2; 1) при минимальном расходе топлива / = 1- Конечного состояния (0; 0) достигнуть невозможно

* Необходимо обратить внимание на отсутствие вьшуклости области достижимости. В связи с этим возникают проблемы при использовании составных скалярных критериев качества.