вого критерия (теорема 10.4) необходимо, чтобы секторы Попова (и/е) f [а, Ь] имели с = = с -d>3 (9,5 дб).

На рис. 10.22 изображена номограмма замыкания с кривыми постоянного усиления

замкнутой системы 20 Ig

H(t) = C-[lCDSLJt

1-Ьг

Здесь же показаны годографы G (/ш) и

а+ b

G{ja)

при значениях = 7,08 (17 дб) н = 28

(29 дб). Выполнение условий кругового критерия (теорема 10.4) для q - Q определяется построением критических окружностей (см. рис. 10.10), которые здесь

определяются условием 20 Ig Для каждого годографа -

Г + Т -201g - - G (/ш) находим кривые

Ь+ а

Рис. 10.21. Система с переменными максимального значения 20 Ig параметрами, соответствующая уравнению Матье (10.45)

6+ о

Ь - а

которые ка-

саются соответствующего годографа. Для годографа

= 1,97; для годографа 28G (/со) 20 Ig

7,08G (уев)-20 Ig Ъ+а

b - a

= 9 56 и

b - a b+ а

= 5,9 дб, или

b+ а

= 2,82.

годографа

b - a a-\-b

7,08

Обратимся теперь к первому годографу 7,08G (/со). Для этого

-i- j = 1,97. Решая совместно эти два уравнения, получим а= 3,5 к b =10,7. Следова-

org(z) (град)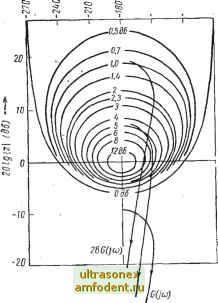

тельно, сектор Попова для годографа 7,08G (/<а)

равен (и/е) (3,5; 10,7). Аналогично определим, g S g что сектор Попова для 28G (/со) равен (и/ё) g £ (18; 38).

Перемещая годограф G (/со) (см. рис. 10.22) в вертикальном направлении, отыщем область возможных секторов Попова, как это показано на рис. 10.23. Область существования абсолютно асимптотически устойчивых управления и выходного сигнала с коэффициентом затухания а = 0,5 сек также показана на рис. 10.23. Эта область получена совершенно аналогично, лишь согласно теореме (10.3) вместо передаточной функции G (/со) используется передаточная функция G (/со - 0,5) (упражнение 10.6).

. 2. Случай, когда q 4= 0. До сих пор критерий Попова исполь-

<Область с декрегеи-

7.08G(SD)

Рис. 10.22. Часть номограммы замыкания, на которой показаны кривые постоянного 1

20 25

значения 20 Ig

1 +Z и arg Z

в функции 20 lg I 2 I

Рис. 10.23. Область асимптотически устойчивого выходного сигнала и управления ограничена кривой а; область с теми же асимптотическими свойствами, но со степенью сходимости а = 0,5 сек ограничена кривой б

зовался для анализа систем, у которых [й, Ь] и q = 0. Перейдем

к анализу систем, для которых (м/е) 6 Ю, Ю и - произвольное число, и покажем, что при этом целесообразно строить годографы KG (/со) в координатах [20 Ig KG (/со), arg G (/со)]. Преобразование прямых Попова с пло-

скости G (/со) на плоскость с координатами [G (}(о)\дб, arg G (/со)] иллюстрируется на рис. 10.24. Покажем, как можно построить это отображение, воспользовавшись номограммой замыкания.

В § 10.3 было показано, что условие Попова (10.20) определяет прямые Попова, показанные на рис. 10.4, а. Сначала рассмотрим случай = 0. Поскольку рассматривается сектор (ы/е)€ [О, К], то для применения кругового критерия необходимо считать с = О, b = К- Прямая Попова соответствует предельной кривой при = = 1 или О дб. Ординаты

на номограмме рис. 10.20 становятся равными 20 Ig 1 G (/со) =

= 20 Ig I KQ (/со I - 6 дб. Поскольку мы стремимся вести построение в координатах 20 Ig /( G (/со) , arg G (/со)], то для получения граничной линии Попова в этих координатах нам достаточно поднять на 6 дб кривую

с параметром ут = О дб. Полученная таким образом кривая изображена

на рис. 10.24, 61).

Отображение прямой Попова для случая (oq ф О показано на рис. 10.24, в и г. В соответствии с рис. 10.24, в уравнение прямой Попова в функции комплексной переменной z =\z\e (где z - текущая точка на прямой)

можно определить через параметр tg 0 = со следующим условием: cos 0 =

= z cos (О - е), где tgQg=q()i: или по-другому

I. I . (е,9со) 1 = ; tgco = е (io.46)

откуда получим

г(е, 90))

г (6-6,0)1 I г (вд, 0) I

20 ig I г (6, 90)) I = 20 ig I г (6 - е 0) I - 20 ig I Z (6 0) . (10.47)

Итак, граничная кривая для aq ф О может быть получена в результате вертикального смещения граничной кривой при 9 = 0 на 201gz(e, 0) и горизонтального смещения на угол = arctg (oq град (рис. 10.24, г). Заметим, что таким образом можно построить семейство граничных кривых для различных значений параметра 0)9; при этом все кривые проходят через точку (-180°, О дб). Семейство кривых показано на рис. 10.25 и является отображением прямых Попова (рис. 10.4, б).

Правило применения рис. 10.25 заключается в том, что для частотной характеристики G (/о)) условие Попова (10.19) теоремы 10.1 вьшолняется, если существует такое действительное 9, что для всех о) годограф G (/оз) расположен ниже граничной кривой, соответствующей (oqK

1) Метод, использующий граничную кривую для оценки условия Попова при д=0, был предложен Б. Н. Наумовым 145]. Он предусматривает построение семейства амплитудно-фазовых характеристик

Gg Ои, 9) = (1 -f jcoq) G (jw)

и проверку условия, располагаются ли они вне области, ограниченной предельной кривой (рис. 10.24, б). Следует заметить, что метод Б. Н. Наумова требует более тщательных построений, чем методы, описанные ниже. Метод, аналогичный методу Б. Н. Наумова, был предложен Марфи [144].

2) Если требуется установить существование асимптотически устойчивого управления или асимптотически устойчивого выходного сигнала с коэффициентом затухания а, то в соответствии с теоремой 10.3 вместо функции G (/со) следует рассматривать функцию G (/ш - а).

Пример 10.14. Для системы, изображенной на рис. 10.1, с однозначной нелинейностью и = f (е) и операторной функцией линейной части

Р р(р + 1)(р+5)

определить максимально возможное значение К такое, что (и/е) g (О, К) и при этом для системы существуют асимптотическое управление и асимптотически устойчивый выходной сигнал. Эта система подобна рассмотренной в примере 10.8 и отличается лишь коэффициентом передачи. На рис. 10.26 дано семейство граничных кривых, показанных также и на рис. 10.25;

arg[G(jl})] грод

z(B.O)

Пряпая Попова для uq = 0

arg[G(jcj)] грод-

25 20

10 %,

nn.KG(]cj)

Прямая Попова для цшФО

18 С-6

Рис. 10.24. Отображение прямых Попова с плоскости G (/ш) на плоскость с координатами {20 Ig KG (jo) , arg G (/ш)}:

а - в полярных координатах на пл. KG (/и) при и 9=0 (как на рис. 10.4); б - отображение прямой рис. 10.24, а при (лд=0; в-в полярных координатах на плоскости KG (/и) при (лд Ф 0; г - отображение прямой рис. 10.24, в при ад Ф О

здесь же нанесен годограф G (/ш). Сдвигая годограф G (ja) в вертикальном направлении, определим соответствующие значения 20 Ig К = 9,5 дб или К = 3,0 и q = 1,2, при которых все точки годографа

20 Ig I KG (/ш) I = 20 Ig I G (ja) + 9,5 дб

лежат ниже граничных кривых Попова 1,2(в при всех значениях ш). Таким образом, для коэффициента К= 9,5 дб = 3,0 условие Попова выполняется. Как и следовало ожидать, полученный результат аналогичен результату примера 10,8, когда для анализа использовался годограф модифицированной частотной характеристики G* (ja)

1) Истинное значение q= 1,2 определяется методом последовательных приближений, но можно воспользоваться плоскостью KG* (ja) для непосредственного отыскания q. Этот способ рассмотрен ниже.