тогда

Xl = XiCO COS co.

a выходной сигнал

и = -x\xi = -X1 ( sin afj ( X jco cos coi) = -хЧ) (---- cos 2at cos со/ =

-j- (cos со/ - cos 3co/). (6.7)

Из выражения (6.7) видно, что выходной сигнал содержит третью гармонику. Предполагая, что третья гармоника достаточно ослаблена линейной частью системы, получим следующее приближенное соотношение:

х\ х\ d г- . , х\

со cos со/ =-----j- (л sin со/) =---рх. (6.8)

Таким образом, если третьей гармоникой можно пренебречь, то прежний нелинейный элемент заменяется эквивалентным в соответствии с равенством (6.8). Его можно рассматри-

вать как дифференцирующее устройство с коэффициентом усиления, пропорциональным xf. Итак, исходную нелинейную систему можно заменить эквивалентной линейной, у которой коэффициент усиления зависит от амплитуды. Тогда наша задача сводится к тому, чтобы исследовать, при каких условиях существуют автоколебания вида х sin со/ для сигнала х эквивалентной линейной системы. Эквивалентная передаточная функция разомкнутой системы имеет вид

(6.9)

а характеристическое уравнение замкнутой системы равно

(хх?о + - (лЯ + 1 = 0. (6.10)

Решая его относительно X, получим

(6. И)

Для существования в контуре автоколебаний х = х sin со/ нужно, чтобы собственные значения или корни характеристического уравнения были чисто мнимьми. Следовательно,

при Xj = 1 имеем Xj = 2, где Я = ±/ и со = 1.

Итак, мы установили, что в системе существуют колебания с амплитудой, равной 2, и частотой 1 рад/сек.

Интересно заметить, что из приближенного решения получены значения амплитуды х и частоты со автоколебаний, не зависящие от ц. На первый взгляд, такой результат невереи. Но из рис. 6.2 и 6.3, где показаны результаты моделирования уравнения Ван-дер-Поля для четырех значений (х ((х = 0; 1; 2; 8), видно, что при выбранных значениях ц приближение оказывается достаточно хорошим.

Постараемся обосновать этот результат, оценив ошибку, которая возникает при допущении о синусоидальном характере колебаний [равенство (6.6) ].

Из соотношения (6.7) следует, что выходной сигнал нелинейного элемента содержит третью гармонику с амплитудой, равной амплитуде первой гармоники. Видно, что, проходя

через линейный блок с передаточной функцией --~-ГТ ( - Р- амплитуда первой

р (хр -р 1

гармоники не изменяется, тогда как третья гармоника ослабляется в - - раз.

Кб4+(3(х)2

Для [Л = 1 ослабление сигнала по третьей гармонике составляет более 18 дб, тогда как первая гармоника не ослабляется вовсе. Таким образом, амплитуда третьей гармоники на входе нелинейного блока (см. рис. 6.1) оказывается почти на порядок меньше амплитуды первой гармоники. Для (х <; 1 предполагаем, что аппроксимация будет еще лучше, тогда как для (X > 1 хуже. Это подтверждается результатами экспериментов, показанными на рис. 6.2 и 6.3.

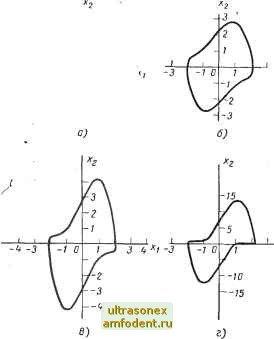2 3 ,

Рис. 6.2. Виды предельных циклов для уравнения Ван-дер-Поля, полученные экспериментальным путем с различными значениями параметра [х:

и-при ti=0; б - при 11=1; в - при ц=2; г - при ц = 8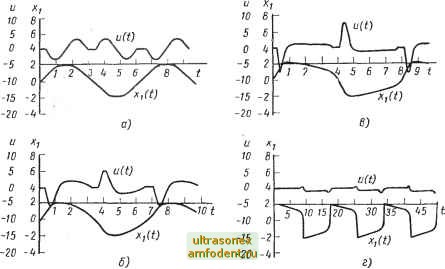

Рис. 6.3. Характеристики переходных процессов Xj и м (f) для системы, изображенной на рис. 6.1, которые получены в результате математического моделирования:

а - при ц = 0: б - при ц = 1; в - при ц = 2; г - при ц = 8

Из-за присутствия третьей гармоники сигнал в точке несинусоидальный. Но предыдущие рассуждения показывают, что при О форма сигнала должна приближаться к синусоидальной, а для (X оо форма сигнала должна в значительной мере отличаться от синусоиды. Все это действительно подтверждается результатами экспериментов (см. рис. 6.2 и 6.3).

Последний вопрос, на который нам хотелось бы ответить, заключается в следующем. Обладает ли полученный предельный цикл асимптотической орбитальной устойчивостью?

На этот вопрос можно ответить, проанализировав уравнение (6.И). Предположим, что х превысила значение амплитуды 2. Тогда из уравнения (6.11) следует, что Я, имеет отрицательную действительную часть. А это означает, что замкнутая система устойчива. И амплитуда

колебаний х убывает. Если же х становится меньше 2, то равенство (6.11) показывает, что система становится неустойчивой, а следовательно, х будет уменьшаться. Таким образом, заключаем, что предельный цикл обладает асимптотической орбитальной устойчивостью.

Изложенный- выше способ определения устойчивости предельного цикла равносилен анализу методом корневого годографа, когда в качестве переменного параметра выбирается амплитуда автоколебаний х. Поскольку предполагается, что \ь системе существуют автоколебания вида

Ху = Xl sin (at, то имеет смысл строить лишь часть годографа вблизи мнимой оси. Корневой годограф гармонически линеа-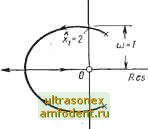

Рис. 6.4. Корневой годограф гармонически линеаризованного уравнения Ван-дер-Поля

ризованной системы в функции х показан на рис. 6.4. Устойчивость предельного цикла можно установить рассуждениями, аналогичными предыдущим.

На практике после выполнения гармонической линеаризации дальнейший анализ системы можно проводить с помощью логарифмических частотных характеристик или частотного годографа *. Все это станет читателю яснее из материала следующего параграфа.

6.2. ]У1ЕТ0Д ГАР]У10НИЧЕСК0Й ЛИНЕАРИЗАЦИИ ДЛЯ CHCTEiVl УПРАВЛЕНИЯ С ОДНОЗНАЧНЬШИ НЕЛИНЕЙН0СТЯ]У1И

В примере 6.1 мы познакомились с методом гармонической линеаризации. У этого метода есть свои истоки. К. Магнус [131], например, показал, что метод связан со многими классическими подходами к анализу Ieлинeйныx систем; в частности, с методами Ритца и Галеркина, переменного параметра, возмущений и гармонического баланса **. Интересно также отметить, что метод гармонической линеаризации - это первый метод, который одновременно применили для анализа нелинейных систем, по меньшей мере, пять исследователей в разных странах *** в период с 1947 по 1950 годы.

В этом разделе мы хотим выявить основу метода гармонической линеари-. зации, связанную с передачей первой гармоники входного сигнала. В одном из последующих разделов мы попытаемся осветить этот метод с другой точки зрения, а именно, исходя из условия минимума среднеквадратической ошибки приближения.

Рассмотрим автономную систему S (рис. 6.5), где предполагается, что нелинейности системы могут быть представлены одним блоком Э. Оставшаяся часть системы G (р) предполагается линейной и стационарной. Поскольку мы будем часто иметь дело с системами, структура которых подобна рис. 6.5, то в дальнейшем такую структуру будем называть стандартной.

* Оба эти метода отличаются простотой и не требуют больших затрат времени при определении автоколебаний в нелинейных системах управления, имеющих высокий порядок передаточной функции линейной части {Прим. ред.).

** Подробное обсуждение этих методов см., например, в работах [37], [143]. *** См. работы [49], [57], [108], [153] и [192].