Следствие 9.2. Теорема 9.6 остается верной и в том случае, если V (х) - знакоотрицательная функция в области но при этом удается показать, что не существует других положений равновесия, кроме начала координат.

Если tfe совпадает со всем фазовым пространством, то следует говорить об асимптотической устойчивости в целом; при этом справедлива следующая теорема.

Теорема 9.7 (Е. А. Барбашин и Н. Н. Красовский) *. Если во всем фазовом пространстве существует для системы 9.4 функция Ляпунова V (х), обладающая тем свойством, что V (х) оо, когда л: оо, и ее производная по времени У{х) определенно отрицательна, то начало координат асимптотически устойчиво в целом.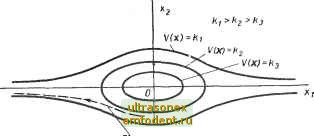

Возпожная траектория Вблизи незапкнутой линии постоянного уровня функции V

Рис. 9.4. Возможная траектория вблизи незамкнутой линии постоянного уровня функции V (штриховая линия)

Следствие 9.3. Если в условиях теоремы 9.7 V (х) - знакоотрицательная функция и при этом не существует других положений равновесия, кроме начала координат, то асимптотическая устойчивость в целом начала координат сохраняется.

Доказательство теоремы 9.7 не представляет труда. По сравнению с предыдущими теоремами в ней лишь используется дополнительное требование, заключающееся в том, что функция V (х) должна стремиться к бесконечности по мере того, как расстояние изображающей точки х от начала координат стремится к бесконечности независимо от направления движения. По!су-ществу это требование должно означать, что поверхности равного уровня функции V{x) являются замкнутыми во всем фазовом пространстве. В противном случае может оказаться, что траектории системы уходят в бесконечность, хотя функция V (х) определенно положительна, а ее производная по времени V (х) определенно отрицательна.

Пример 9.8. Допустим, что в достаточном удалении от начала координат линии одного уровня оказались незамкнутыми. Заметим, что линии постоянного уровня обязательно замкнуты вблизи начала координат при условии, что функция V (х) определенно положительна, а ее производная V (х) определенно отрицательна. На рис. 9.4 показаны соответствующие кривые постоянного уровня для системы второго порядка. Здесь же приведена возможная траектория системы, уходящая в бесконечность, которая приближается к линии постоянного уровня, но никогда не совпадает с ней.

* См. Барбашин Е. А. Введение в теорию устойчивости . Наука . М., 1967. Барбашин Е. А., Красовский Н. Н. Об устойчивости движения в целом . ДАН СССР, 1952, т. 86, вып. 3 (Прим: ред.).

Например, для функции V (х) вида

п

1/ (X) = S Vi (xi), 1=1

когда один или более, но не все У; имеют конечный предел при xi сх>(например, Vi (xi) =

=-гг , существуют незамкнутые поверхности постоянного уровня (покажите это).

Пример 9.9. Вернемся вновь к анализу движения математического маятника (пример 9.3). Поскольку выбранная выше функция Ляпунова

1/(9, e) = --(l-cose)-f-l-e2

совпадает с полной энергией системы, то существует достаточно большая область, в которой функция V не имеет максимума *. Указанная область ограничена сепаратрисой, т. е. траекторией, которая начинается сколь угодно близко к точке Gq = ±п,; Gq = 0. В этой области

функция V ограничена значением 2 j-, которое равно величине потенциальной энергии в точке

Go = ±я. Go = 0. Таким образом, условия следствия 9.2 выполняются,и поэтому положение равновесия задемпфированного математического маятника асимптотически устойчиво в большом в указанной области.

В данной конкретной задаче нам удалось отыскать область асимптотической устойчивости в большом, которая совпадает со всей областью начальных условий в силу специфики самой задачи. Как правило, этого не случается.

Пр и м е р 9.10. Управление углом тангажа спутника, который стабилизирован грави-тационньми силами **. При движении по круговой орбите спутника, имеющего гантельную форму, возникают медленные колебания относительно центра масс. Это связано с тем, что существует небольшая разница в силах гравитации, воздействующих на нижнюю и верхнюю гантели; возникающий при этом стабилизирующий момент и приводит к указанньм колебаниям. Было предложено большое число схем, в которых для стабилизации использовались гравитационные силы. Покажем, каким образом можно за счет активных сил задемпфировать возникающие из-за градиента гравитации колебания.

Запишем линеаризованные уравнения углового движения спутника в плоскости тангажа в следующем виде:

JxQ+iQ{J2-Jb)Q= u(t), . (9.12)

где Ji, 2 и /з - моменты инерции спутника соответственно для движения тангажа, крена и рыскания;

Q - угловая скорость орбитального движения; , .

G - отклонение угла тангажа от направления местной гировертикали. Наша задача заключается в том, чтобы синтезировать систему с обратной связью, т. е. сформировать управление и в функции y..-ловой скорости 6 и угла тангажа G таким образом, чтобы колебания относительно центра масс были задемпфированы.

В том случае, когда управление и формируется в виде линейной комбинации сигналов G и 6, задача получается тривиальной, поскольку вся система оказывается линейной. Рассмотрим возможность формирования управления в виде и = -f (aG -- PG), где функция / удовлетворяет условию

f (0) = 0; xf (х) > О, если x=j=0; (9.13)

это означает, что график f {х) расположен только в первой и третьей четвертях плоскости (/ {х), х) и проходит через начало координат.

Образуем функцию Ляпунова V (9, G) в виде

ае-ьрё

У(0, G) =(G2-f а62) -f 6 f{l)dl, а>0, b >0,

Это подразумевается и в условиях теоремы 9.6 (см. упражнение 9.12). Более подробно эта задача рассматривается в работе [82].

Тогда

V (9, ё) = ее + йб еч- 6 ( ё + рё) / ( е + рё) = (i - щ её - (--ба)ё + бре

Если выбрать величину а = i, а 6 = j k ° сражение для V упрощается:

Поскольку нелинейная функция удовлетворяет условию (9.13), то ясно, что при а> О и р > О функция V будет определенно отрицательной, а начало координат (е = О, ё = 0) асимптотически устойчиво.

Если а = О, то 1/ - знакоотрицательная функция. Однако и в данном случае начало координат есть единственное положение равновесия; другие точки, где V = О, не являются положениями равновесия (ответьте - почему?). Таким образом, начало координат системы (9.12) по-прежнему асимптотически устойчиво, когда управление и - -f (рё), где функция f удовлетворяет условию (9.13).

Наконец, рассмотрим случай, когда f (х) удовлетворяет условию

/(x)rfx=oo;

это условие вьшолняется, например, для нелинейного элемента с насыщением; при этом V (е, 6) -> оо, когда (е -\- ё) -> оо, и, следовательно, начало координат системы асимптотически устойчиво в целом. Но поскольку изучаемая математическая модель получена в результате линеаризации, то эта модель верна лишь для малых сигналов. Поэтому свойство асимптотической устойчивости в целом для исходного объекта может и не выполняться.

9.4. ФУНКЦИИ ЛЯПУНОВА ДЛЯ ЛИНЕЙНЫХ ABTOHOiИHЫX CHCTEJVi

Для линейной автономной системы существование функции Ляпунова в виде квадратичной формы переменных состояния является одновременно необходимым и достаточным условием равномерной асимптотической устойчивости в целом [98], [118], [130].

Рассмотрим линейную стационарную систему

х = Ах. (9.14)

Допустим, что нам удалось найти функцию Ляпунова в виде квадратичной формы V [х) = xQx, где матрица Q симметрична и положительно определенна *. Тогда

V{x) = xQx + xQx = xAQx + xQAx = jc {AQ + QA)x. (9.15) Обозначим

AQ + QA=- - C, (9.16)

тогда поскольку матрица С положительно определенна, то система асимптотически устойчива в целом; более того, так как

С- = - {AQ + QAf = - {QA + ЛQO = - Ш +AQ) = ~C, то матрица С также и симметрична.

* См. приложение I.