Теорема 9.5 (теорема Четаева о неустойчивости). Пусть Ы - произвольная окрестность начала координат, а Мх - область внутри М. Допустим, что найдена функция Y (х), такая, что:

1) функция имеет непрерывные частные производные первого порядка в области Ых,

2) функции У (х) я V {х) определенно положительны в области М, состоящей из внутренних точек области

3) на границе Ы-х V (х) = 0;

4) начало координат принадлежит границе области Мх- В этих предпосылках начало координат неустойчиво.

Доказательство (рис. 9.2). Условия теоремы означают, что траектории системы, начинающиеся в области не могут пересекать границу IQ этой области, объединяющую внутренние точки области Ы. Однако из условия теоремы также следует, что изображающая точка должна покинуть область Ых и это может произойти лишь при движении по границе Му, не совпадающей с fi. Таким образом существуют две разновидности граничных точек области Ых- одни являются внутренними точками области М, образуя границу IQ; другие, являясь граничными для обеих областей, образуют линию IQ.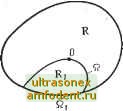

Рис. 9.2. Геометрическая интерпретация условий теоремы Четаева о неустойчивости. Область 91х принадлежит области SI; при этом они расположены по разные стороны от .границы Q и по одну и ту же сторону от границы Qi

Пример 9.3. Уравнение движения математического маятника единичной массы можно записать в виде

е Х sin е = о.

(9.5)

где g - ускорение силы тяжести; L - длина маятника. Для анализа устойчивости определим функцию V следующим образом:

к(е, ё)=-f-(i-cose)+-ё (9.6)

Заметим, что функция V (6, 6) определенно положительна для всех б <; 2я, и

-KM. = -f Sin е.еЧё(- Sine), 0.

Введенная таким образом функция V является функцией Ляпунова, и, следовательно, по теореме 9.1 положение равновесия математического маятника устойчиво.

Функция V (G, G), удовлетворяющая уравнению (9.6), пропорциональна полной энергии системы, которая по определению является определенно положительной функцией. Кроме того, поскольку система (9.5) консервативна (см. гл. 4), то ее полная энергия будет сохраняться, и, следовательно, функция тождественно равна нулю. Этот пример показывает, что все консервативные системы устойчивы, поскольку их полная энергия является функцией Ляпунова.

Пример 9.4. Допустим, что движение математического маятника задемпфировано так, что уравнение движения принимает вид

e-f Ш -

sin е = 0; k> 0.

(9.7>

Снова задаваясь функцией Ляпунова V (6, 6), по уравнению (9.6), находим, что

V = -кв (9.8>

и является знакоотрицательной функцией, так как V отрицательна всюду, кроме точек с координатами ё S О, где F = 0. Таким образом, очевидно, что решение дифференциального уравнения (9.7) устойчиво. Кроме того, отметим, что лишь при 6=0 вьшолняется условие в = 0. Следовательно, можем сделать вывод, что система (9.7) обладает и свойством асимптотической устойчивости.

Следствие 9.1. Если в области , включающей начало координат, существует функция Ляпунова, производная по времени от которой в силу уравнений движения является знакоотрицательной функцией, и если можно показать, что ни одна из точек, где V = О, кроме начала координат, не является положением равновесия, то начало координат асимптотически устойчиво.

Пример 9.5. Первый метод Ляпунова бьш изложен в гл. 5; основополагающее значение имела теорема 5.1, теперь есть возможность доказать ее. Пусть задана система вида

x = Ax + h{x), (9.9)

где lim ( h (х) / х ) = О, т. е. h (х) -> О быстрее, чем х Ц. II К о

Случай 1. Пусть собственные значения матрицы А для линеаризованной системы (9.9) вида х= Ах являются действительными, различньми и отрицательными; тогда линеаризованная система асимптотически устойчива и остается показать, что исходная нелинейная система (9.9) также асимптотически устойчива.

Во-первых, следуя гл. 3, находим преобразование у = Рх такое, что

y = Ay+h{y), (9.10)

где, как и ранее, Л есть диагональная матрица, составленная из собственных значений матрицы А. Допустим, что

тогда

п п п

1>(У) = 22 i,- = 2S {yc[hyi+hi{y,t)]] = 2%iy1 + g(y,t), (9.11)

i=I t=I /=1

где§(у, ) = 2 у A (У i)-

Заметим, что !§(} , ) -> О быстрее, чем у P, для каждого i. Таким образом, в достаточно малой окрестности начала координат первый член в правой части соотношения (9.11) будет доминирующим и V (у) будет определенно отрицательной функцией. Следовательно, по теореме 9.2 начало координат асимптотически устойчиво.

Случай 2. Пусть некоторые из корней, скажем Х, . . ., h (1<С п), положительны и различны, а остальные отрицательны и тоже различны. Тогда линеаризованная система неустойчива. Чтобы показать, что нелинейная система также неустойчива, возьмем

V = y\ + ---+yi-y\i-----У

тогда

V = 2 {\у\ + + Цу]-h+iy+i-----Ку1) +8(УП-

В некоторых точках, вблизи начала координат, а именно в тех, где = у =...-

= №= О, К> 0; к тому же V в точках, очень близких к началу координат, определенно положительная функция и, следовательно, по теореме 9.3 начало координат неустойчиво. Случай комплексных корней рассмотрен в упражнении 9.3. Пример 9.6. Рассмотрим систему

= axl + bxl; \ = -сх + dxf, где а, Ь, с, dy-0.

в результате линеаризации получим систему с полюсами в точках О и (-/). Здесь мы имеем критический случай, когда первый метод Ляпунова применять нельзя. Определим

функцию V = Ху - ( ~) которой с учетом уравнений системы получим V = Ху - 2X2 = + bxl) - 2 {-сх + rfxj).

Рассмотрим рис. 9.3. В незаштрихованной области, ограниченной Кривой Jt;j = -,

в точках которой V = О, функция У > 0. Кроме того, внутри этой области в точках, доста. точно близких к началу координат, знак функции V будет определяться знаком функции аху -j- cx, и, следовательно, V в этой области определенно положительная функция. Условия теоремы Четаева о неустойчивости, таким образом, выполняются, и начало координат неустойчиво, согласно теореме 9.5.

Пример 9.7. Рассмотрим систему

Ху = Х2 + ху (4 -I- 4); 2 = + 2 (4 + 4)-

В результате линеаризации можно получить х-у = Xzl х = = -х. Корни характеристического уравнения комплексно сопря-женны и равны Х= ± j. Вновь имеем дело с критическим случаем, когда первый метод Ляпунова неприменим. Определим функцию Ляпунова следующим образом:

Рис. 9.3. Функция Ля- Т + 2) (1 + 2) +4)-

пунова для примера 9.6

Тогда обе функции V к V определенно положительны. Условия теоремы 9.3 выполнены, и, следовательно, начало координат неустойчиво.

9.3. ТЕОРЕМЫ ОБ УСТОЙЧИВОСТИ В БОЛЬШОМ И УСТОЙЧИВОСТИ В ЦЕЛОМ

Основное преимущество второго метода Ляпунова заключается в том, что этот подход нетрудно распространить для анализа асимптотической устойчивости в большом и асимптотической устойчивости в целом [118].

Ведь если в процессе анализа или синтеза системы оказалось возможным установить свойство асимптотической устойчивости в большом или, быть может, даже в целом, то уверенность проектировщика в работоспособности такой системы еще более возрастает, хотя следует ясно представлять, что изучаемая математическая модель системы редко оказывается справедливой во всем фазовом пространстве или при произвольных начальных условиях. И в этом смысле установление факта устойчивости в целом может вызвать ложное чувство успокоенности. Вот почему анализ устойчивости в большом полностью оправдан только в том случае, когда изучаемая модель адекватна объекту во всем диапазоне исследуемых начальных условий.

Сформулируем основную теорему об асимптотической устойчивости в большом, предварительно совместив положение равновесия системы с началом координат.

Теорема 9.6. Пусть в ограниченной окрестности начала координат функция V (х) для системы (9.4) меньше постоянной величины k. Если в области функция V (х) есть функция Ляпунова, производная по времени от которой V (х) определенно отрицательна, то начало координат (положение равновесия системы) асимптотически устойчиво в большом в области с.

Доказательство почти аналогично доказательству теоремы 9.2, и мы предлагаем читателю проделать его самостоятельно.

Справедливо также следствие.