ВыхоВ

утверждение, рассмотрев несколько других двузначных нелинейностей. Отметим также, что при а = О рассматриваемая нелинейная характеристика переходит в релейную. Однако следует быть осторожным в определении знака фазового сдвига, который зависит от того, является ли линейный двузначный элемент пассивным или активным .

Чтобы лучше понять высказанную мысль, мы прежде всего дадим определения терминам -- пассивный и активный. Двузначная нелинейность называется пассивной, если за один период входного сигнала нелинейная характеристика обходится против часовой стрелки (рис. 6.11, а). Если же при тех же условиях нелинейная характеристика обходится по часовой стрелке, то двузначный нелинейный элемент является активным

(рис. 6.11, б). Исходя из этих определений нетрудно понять, что пассивная нелинейность всегда приводит к фазовому запаздыванию, а активная - к фазовому опережению.

Мы видели, что некоторые однозначные нелинейности не приводят к фазовому сдвигу, а некоторые двузначные нелинейности его вызывают. Это наводит на мысль, что эквивалентная передаточная функция однозначной нелинейности есть действительная величина. Последнее положение мы и сформулируем в качестве теоремы. Теорема 6.1. Эквивалентная передаточная функция любой однозначной нелинейности есть действительное число.

Доказательство. Рассмотрим некоторую произвольную нелинейность (например, рис. 6.11, а), на входе которой действует гармонический сигнал X {t) = х (t) = X sin со/, тогда выходной сигнал и {t) можно представить рядом Фурье

и (О = 1 sin со/ + Pi cos со/ + ...

По определению эквивалентная передаточная функция задается соот-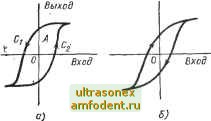

Рис. 6.11. Гистерезисные характеристики нелинейных элементов:

а - для пассивного; б - для активного

ношением

A?(J)A3. + /i.

Д 1

c[x (/)] Sin со/d (со/);

(6.33)

(6.34а)

Pi = 1 [Хп (01 cos со/ d (со/).

(6.346)

Поскольку = X cos со/, соотношение (6.346) можно записать

в следующем виде: 1 Г

[Х (/)] dx, (/) + [X, (/)] dx, (/)] = .

С,+С

кривые Cl и с2, показаны на рис. 6.11, с.

lx{t)]dx{t)

(6.35)

Очевидно, что выражение в скобках в соотношении (6.35) определяет площадь А, ограниченную кривыми и С,- Отсюда следует, что

Pi ==-4- или 1тЛ?(;0 = -4-. (6.36)

лх пх

Таким образом, мнимая часть эквивалентной передаточной. функции {х) пропорциональна площади, ограничиваемой гистерезисной характеристикой. Для однозначных нелинейностей отсюда следует, что Im (х) = == 0. Этим и доказана теорема.

Отметим, что, вообще говоря, площадь Л, ограничиваемая характеристикой пассивного нелинейного элемента, есть мера энергии, которая рассеивается за один период. Таким образом, вводя пассивную нелинейность в систему, мы тем самым увеличиваем степень демпфирования.

Эквивалентные передаточные функции для некоторых часто встречающихся двузначных нелинейностей приведены в табл. 6.2 (строки и 20-27).

6.4. ОБЩИЙ МЕТОД ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ОДНОЗНАЧНЫХ НЕЛИНЕЙНОСТЕЙ

До сих пор понятие эквивалентной передаточной функции использовалось лишь для случая синусоидального входного сигнала. Сейчас мы рассмотрим еще одну трактовку эквивалентной линеаризации, которая применима для более широкого класса входных сигналов; Ясным по интуиции и аналитически приемлемым по своим выкладкам является определение эквивалентной передаточной функции на основе минимизации среднего квадрата ошибки воспроизведения заданного входного сигнала. При таком подходе входными сигналами могут быть различные периодические и даже случайные сигналы. При синусоидальном входном сигнале мы получим результаты, соответствующие методу гармонической линеаризации. Это следует непосредственно из условия ортогональности функций, по которым строится разложение Фурье. Наконец, указанный подход без труда переносится на случаи, когда имеется несколько входных сигналов.

Рассмотрим однозначные нелинейности, описываемые следующим соотношением:

y = f{x). (6.37)

Предполагая, что входной сигнал имеет вполне определенную форму X {f) = Xl {f) (в частности, это может быть периодическая функция х (t)), отыщем эквивалентный элемент, который обеспечивает следующее равенство:

yAt) = N{Xi)Xi, (6.38)

где матрица эквивалентных передаточных функций Л, зависящая от некоторых параметров вектора Xi{t), выбирается таким образом, чтобы минимизировать среднее значение квадрата разности между действительным входом / {Xi) и приближенным выходом (6.38). Это означает, что если

e(f)= f{Xi)-Nixj)Xi, (6.39)

то N (jti) выбираем так, чтобы минимизировать средний квадрат некоторой нормы для ошибки

8(0P = lim е(01Г- (6.40)

Такой подход иллюстрируется с помощью рис. 6.12. Отметим, что

+ xlNNxi,

(6.41)

где черта сверху означает усреднение по определению (6.40). -1* Минимизацию величины е

по параметрам N- можно выполнить, беря частные производные д\\е\f/dNij и приравнивая их к нулю. В результате получим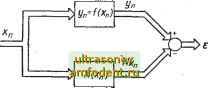

Xij = 0. (6.42)

Следовательно,

(t, /=: 1, n).

(6.43)

Рис. 6.12. Структурная схема, поясняющая эквивалентную линеаризацию (в векторном виде) на основе метода минимума - Поскольку величины XikXij и fiXij усредненного квадрата ошибки выходного можно ВЫЧИСЛИТЬ, то из уравнения сигнала для заданного входного сигнала /п лп\

(6.43) находим эквивалентные передаточные функции Nik-

Пример 6.6. Рассмотрим случай одномерной нелинейности. Здесь - скаляр, и уравнение (6.43) принимает вид

Л/ = или Л/ = . (6.44)

Если входной сигнал х = xsin со, то для вычисления по соотношению (6.44) имеем

fXx =

[f {х sin Ш)] sin (ut d ((at)

Ч--9--

Таким образом, функция

N(x) =

2л nx 0

sin at)] sin co d (cot)

(6.45)

определяет эквивалентную передаточную функцию, рассмотренную в предыдущем параграфе.

Пример 6.7. Рассмотрим случай нелинейности с двумя входами хц и и одним выходом. В этом случае

= + +Т + 2N N,2XnXi2 ~ 2NnHif - 21212/.

Для отыскания минимума найдем деУдЫ и dBldNi и приравняем их нулю. Это даст Nxn + Л?12ЗД2 = (6.46а)

111Л2 + Л12 = (6-466)