ческая устойчивость выполняется, поскольку lim бх = 0. Однако при Xg = (2m + 1) it урав-

<->со

некие (5.6) преобразуется к виду бх = бх, что соответствует расходящемуся процессу, и, следовательно, такие положения равновесия неустойчивы.

Итак, в рассмотренном случае анализ линеаризованной системы позволяет решить полностью вопрос об устойчивости исходной нелинейной системы.

Теперь достаточно просто распространить процедуру линеаризации на системы п-го порядка при постоянных входных сигналах. Рассмотрим стационарную линейную систему

x=f{x, и).

(5.7)

где функция / (л:, и) предполагается непрерывно дифференцируемой по каждой из переменных х и и.

Если управление тождественно равно нулю или постоянному вектору и о, то положения равновесия, задаваемые вектором х, определяются из уравнения

Пусть

0 = /(jf Ио).

x{t) = Xe + 8x{t); u{t) = Uo + 8u{ty, X (t) = Хе + бх (ty, 8х (t) = бл: (О,

(5.8)

(5.9)

где 6х (t) и 8и (t) - возмущения по Хе и Uq соответственно, а 8х (f) есть производная по времени от 8х (f).

Подставляя соотношение (5.9) в первоначальное уравнение (5.7) и вычитая выражение (5.8), получим уравнение возмущенного движения системы в виде

8х {t) = f{x, 8х (ty Uo + би (0).

(5.10)

Поскольку функция / предполагается непрерывно дифференцируемой по своим аргументам, уравнение (5.10) можно представить в виде

8х =-{Хе, Ио) бл: + (л: Uo) 8u-h (л: о, блг, би), где ~- (Хе, и о) и -~ (Хе, о) зздаются матрицами Якоби

(5.11)

дк dfx

дхх дх2

dfn dfn

дХх

dfn dux

дХп.

(5.12а)

х=х и=ч

dfn dur.

(5.126)

K=Uo

x=x

и h (Xg, Uo, 8x, 8u), или сокращенно h (блг,би), представляет остаточный член.

Теперь предположим, что если бл: и 8и стремятся к нулю, то h стремится к О быстрее, чем линейные члены в правой части уравнения (5.11). Точнее говоря, будем считать*, что

ll6uK0 l6u4.0

(5.13)

тогда в достаточно малой окрестности лг и для малых би , поведение возмущенной системы можно описать линеаризованным уравнением

(5.14)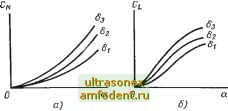

Рис. 5.5. Типовые зависимости для безразмерных аэродинамических коэффициентов примера 5.6:

а - для Сд,; б - для С ; е - для С

Поскольку полученное уравнение линейно и стационарно, то его анализ значительно упрощается. При этом можно воспользоваться любым из известных методов исследования линейных систем. Обратимся к примеру.

Пример 5.6. Линеаризованные уравнения движения ракеты. На рис. 2.15 показана простейшая крылатая ракета, движущаяся в плоскости после завершения этапа разгона. Теперь мы подготовлены к тому, чтобы вывести линеаризованные уравнения движения ракеты. Полные уравнения дви>;;ения задаются в виде

Jb= AIQCm (а, 6); mVy = AQCl {а, 6); mgUN = AQCn (ос, 6),

(5.15a) (5.156) (5.15в)

где См, Сс, Cn - безразмерные коэффициенты момента, подъемной силы, перпендикулярной к вектору скорости, и нормальной силы соответственно; А, I - приведенная площадь и длина соответственно; в нашем примере полагаем А и / равными единице. Безразмерные коэффициенты задаются в виде кривых в функции величин а и 6, полученных в результате аэродинамических продувок. На рис. 5.5 показаны типовые зависимости для коэффициентов См, С и Cn-

Первое уравнение есть уравнение моментов, второе - уравнение сил по направлению к нормали вектора скорости снаряда и третье - уравнение боковых сил.

Этих уравнений вполне достаточно, чтобы описать динамику ракеты. В частности, попробуем оценить влияние малого отклонения управляющих органов на изменение кривизны траектории В и величину поперечного ускорения а- Поскольку Q = а-\- у, выберем 6 и а в качестве переменных состояния. Тогда из первых двух уравнений получим

= -гСм (а. 6);

(5.16)

* Если / (х, и) можно представить рядом Тейлора относительно переменных и ио и h фх, 6и) содержит члены со степенями 6х и 6и второй степени и выше, то в этом случае можно считать, что уравнение (5.13) удовлетворяется.

Условие балансировки заключается в-том, что значения величин а - а; 6 = бу и 6 = ej. обращают левые части уравнения (5.16) в- нуль, т. е.

О =-J-(%, бу); 0 =

CL(ar.6,)+eft.

(5.17)

Совокупность значений а, б. и 6 таким образом определяет положение равновесия * в рассматриваемой системе. В частности, из физических соображений следует, что совокупность = 6j. = бу = О должна соответствовать положению равновесия. Для анализа движения системы относительно у = 6 = бу = О обозначим 66 = 6; 6а = а и т. д. Линеаризованные уравнения в этом случае можно записать в виде

6 =

да dCL

dCt дЪ

6=0 J

6=0 .

(5.18)

Следуя принятым обозначениям, получим дСм

Смг. =

дСь

± дСь

Запишем уравнения Q

(5.19)

(5.20)

позволяющие найти величины а и 6 в функции от 6.

Если в качестве выходной-координаты использовать величину поперечного ускорения, то следует воспользоваться уравнением (5.15в). Линеаризуя его вблизи точки а,. = 6у = ёу = = О, получим

где, как и раньше.

dCN дд,

(5.21)

(5.22)

Частные производные обычно вычисляются непосредственно по кривьм, полученным в результате продувки. Уравнения (5.20) и (5.21) представляют собой линеаризованные уравнения движения ракеты при малых отклонениях от положения равновесия.

5.4. ПЕРВЫЙ МЕТОД ЛЯПУНОВА АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ ОТНОСИТЕЛЬНО ПОЛОЖЕНИЯ РАВНОВЕСИЯ

Первый метод Ляпунова - это по существу теорема, определяющая условия, при выполнении которых устойчивость исходной системы можно анализировать с помощью простых уравнений, полученных в результате линеаризации. Теорема изложена в первой части широко известной диссертации, завершенной в 1892 г. великим русским математиком А. М. Ляпуновым [130].

Теорема в том виде, как она обычно формулируется, справедлива лишь для автономных систем, и поэтому прежде чем приступить к изложению

* Читателю следует помнить, что в этом простейшем примере рассматривается движение ракеты в однородной атмосфере. В противном случае состояние равновесия будет зависеть от времени, и трудности в анализе существенно возрастут.