Когда е> 1, то система периодически выходит на ограничение. Используя эквивалентную передаточную функцию нелинейного звена, можно записать

/? (со) = £ (со) + N (е) eG (/со), (6.64)

где, согласно § 6.2, для нелинейности с единичным уровнем ограничения имеем

arcsin- / 1

(6.65)

Равенство (6.64), в сущности, определяет условие баланса по первой гармонике. Из него видно, что анализ удобнее проводить, приняв за аргумент

амплитуду е. Исходя из этого обозначим R через R (со, ё).

Используя соотношения (6,64) и (6.65), можно построить годограф R (со,

е) для заданного со и дяя 1 = е < оо. Такой годограф обозначен на рис. 6.18, а буквой Г. Поскольку (е) е-монотонно возрастающая функция, ограниченная сверху величиной -, то можно предположить, что годографимеетвид,

изображенный на рисунке.

Заметим, что для системы, структурная схема которой показана на рис. 6.17, можно построить годограф Г для каждой фиксированной частоты со. Такое геометрическое построение позволяет выявить явление скачкообразного резонанса на определенной частоте со.

Для частного случая, изображенного на рис. 6.18, а, обозначим вектор R (со, 1) через R, а точку, где годограф Г пересекает мнимую ось, - через R. Прежде всего проанализируем, что происходит при увеличении

амплитуды г.

Если I Rs I станет больше /?с , то существует значение \ R\, обозначенное, как I Rm 1, которое лежит на отрезке годографа Г между R и Rc и обладает тем свойством, что оно является максимальным из всех \ R \ иа этом отрезке. Если R превысит хотя бы незначительно R \, то условие (6.64) удовлетворяется только в том случае, когда вектор R изменит скачком свое направление, перейдя из точки 1 в точку 2 (рис. 6.18, б). Однако такое изменение вектора R приведет к скачку модуля векторов Y и Е. Этот результат соответствует скачку АБС {см. рис. 6.16). Таким образом, рабочая точка системы не может находиться на сегменте Г между Rm и Rc.

Посмотрим теперь, что происходит, если г уменьшается, имея начальное значение, большее чем Rm]- Из рис. 6.18, б видно, что всякая точка годографа Г, лежащая правее R может быть рабочей точкой системы. Но поскольку /?с определяет теперь минимум, то как только R уменьшается до значения R, происходит мгновенный перескок из точки 3 в точку 4, при котором вектор R меняет лишь направление. При этом Y и Е должны скачком изменить амплитуду. Это соответствует скачку СЕЛ (см. рис. 6.16).

Отметим, что точки отрезка. BFE как амплитудной, так и фазовой характеристик на рис. 6.16 представляют возможные точки работы системы, но в действительности система в них не работает. Это неустойчивые точки.

Исходя из геометрической интерпретации явления скачкообразного резонанса можно сделать следующие выводы (упражнение 6.10)*.

* При условии, что метод гармонической линеаризации применим. Это предположение сохраняет силу на протяжении всей главы.

Область В

1. Явление скачкообразного изменения у в функции от г при фиксированном (о происходит лишь в том случае, если Re < О и существует вектор Rm с максимальной амплитудой.

2. Если Re G (/со) > -1 для всех со, то явления скачкообразного резонанса не наблюдается,

3. Достаточное условие скачкообразного резонанса на частоте со связано с попаданием годографа G (/coi) в область В (рис. 6.19), которая огра-

ImCijcj)- ничена справа двумя прямыми, обозначенными через Л; когда это условие выполняется, скачкообразный резонанс может быть обусловлен любым возмущением в системе, даже если до этого система работала в линейной области.

Поскольку условия 1) и 12) являются необходимыми и достаточными для существования скачкообразного резонанса, то они определяют и единственным образом границу области, где это явление имеет место. Последняя может быть построена графически или определена численно. На рис. 6.19 граница обозначена через Й. Как правило, скачкообразный резонанс - явление нежелательное, и поэтому годограф Q определяет ограничение, которое ралагается на частотную характеристику G (/со) для предотвращения такого явления. Ограничение заключается в том, что годограф G (/со) для всех со должен располагаться правее кривой Q. В этом случае существует единственная эквивалентная передаточная функция замкнутой системы (рис. 6.17) при заданном синусоидальном входном сигнале г (f). Она зависит как от амплитуды, так и от частоты (см. упражнение 6.11). Оказывается возможным перенести предлагаемый метод анализа и на другие нелинейности и построить годограф jfi для этих систем *. Дальнейшее развитиеТуказанной методики дано в работах Хатанака [71 ] и Фукума и Мацубара [55 L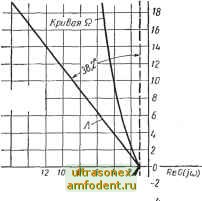

Г6 к

-16 -IB

Рис. 6.19. Кривые, определяющиеобласти существования скачкообразного резонанса

6.6. ЗАПАС ПО АМПЛИТУДЕ В НЕЛИНЕЙНОЙ СИСТЕМЕ И ЕГО ПРИМЕНЕНИЕ В ЗАДАЧАХ СТАБИЛИЗАЦИИ СИСТЕМ УПРАВЛЕНИЯЗ ; НЕЛИНЕЙНЫМИ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ

в этом параграфе рассмотрим пример, иллюстрирующий изложение материала предыдущего параграфа и обобщающего большой класс систем, часто встречающихся на практике. Изучим сначала систему с обратной связью, в состав которой входит рулевой привод. Структурная схема такой системы показана на рис. 6.20.

* В гл. 11 мы покажем, что кривая Q, полученная на основе метода гармонической линеаризации, всегда определяет большую область возможнцх расположений годографа G (/со), нежели при анализе точными методами.

Нелинейный привод является одной из основных причин, ухудшающих свойства системы управления. Некоторые его, на первый взгляд существенные, преимущества оказываются обманчивыми. Так, например, диапазон входных амплитуд, при которых привод в целом ведет себя как усилительное звено, очень незначителен. Поэтому, когда проектировщик оценивает свойства привода только с точки зрения усиления, то может впоследствии обнаружить, что хотя система и устойчива в малом, но в силу любой случайности (например, при появлении входного сигнала) она становится неустойчивой или в ней возникают нежелательные колебания. Даже если этого не произойдет, качество действительной системы будет значительно отличаться от предполагаемого. Ниже мы покажем, что при этом происходит

G,(P)

\Корректиру-

кщее устройство

ПределЫЦ] t)

u(t)

Привод.

Бр(р)

Рис. 6.20; Структурная схема системы управления с рулевым приводом

И какие меры может предпринять проектировщик, чтобы исключить возможность возникновения колебаний.

Вообще говоря, в правильно спроектированной системе как положение, так и скорость рулевого привода должны находиться как можно дольше на уровне ограничения для того, чтобы максимально использовать возможности привода.. Когда сигнал управления значителен, привод, в основном, характеризуется- уровнями ограничения по положению и скорости; например, в гидравлическом приводе такие ограничения соответствуют максимальному ходу плунжера и максимальному расходу рабочей жидкости.?

Для значительных по уровню сигналов хорошее приближение к действительному поведению привода может дать его модель, показанная на структурной схеме рис. 6.20 *. Для отдельно изображенной на рис. 6.21, а модели привода эквивалентная передаточная функция \ показана на рис. 6.21,6** (см. также упражнение 6.12),

Пример 6.9. Проанализируем систему, структурная схема которой показана на рис. 6.20, если привод имеет характеристики, изображенные на рис. 6.Й1 б, а передаточная функция объекта задана соотношением

(6.66)

Сначала рассмотрим, что произойдет, если спроектировать систему исходя из того, что она работает при малых сигналах управления. Для таких уровней сигнала привод можно описать усилительным звеном с единичным коэффициентом усиления. Тогда можно найти корректирующую цепь, которая обеспечит удовлетворительное качество процессов в замкнутой системе.

* Отметим, что на рис. 6.20 показано как ограничение по положению привода, равное ± и, так и ограничение по скорости ±/.

** Кривая, показанная штриховой линией на рис. 6.21, б, представляет частотные характеристики привода с обратной связью, справедливые лишь при малых входных сигналах. При значительной амплитуде эквивалентные частотные характеристики будут в большей степени соответствовать рассматриваемой модели.