в частности, совсем просто строить фазовые портреты линейных автономных систем второго порядка (см. § 4.3). Отметим, что при достаточно общих условиях (теорема 4.1) для таких систем существует единственное положение равновесия в начале координат. Знание траекторий линейной системы вблизи начала координат окажет большую услугу при линеаризации нелинейных систем.

Для нелинейных автономных систем второго порядка характерно существование либо предельного цикла, либо множества положений равновесия (даже зон равновесия), и, наконец, для одной и той же нелинейной системы может существовать несколько видов траекторий (§ 4.4). Общие методы построения фазовых портретов разработаны только для консервативных систем (§ 4.5).

Однако известно большое число методов, которые позволяют произвести приближенное построение фазовых траекторий (§ 4.6). Независимая переменная - время, как правило, не обозначается на фазовых траекториях, но существуют методы, которые позволяют оценить время протекания переходных процессов по фазовым портретам (§ 4.7).

Пределы применимости метода фазовой плоскости очевидны; он неприемлем для анализа систем высокого порядка и неавтономных систем *.

4.9. ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ

4.1. Уравнение Ь + юб = -В sign 6 описывает динамику системы с кулоновым трением. Постройте фазовые траектории этой системы.

4.2. Постройте фазовые траектории в нормальных координатах для следующих систем: а) X-\- XXX = 0;

6)х + х + х = 0.

Дайте наглядную интерпретацию полученным результатам.

4.3. Методом изоклин постройте фазовые траектории для линейной автономной системы второго порядка с кратными действительными корнями, меньшими нуля. .

Указание Воспользуйтесь каноническими переменными, для которых

где k - постоянная и X < 0.

Какое влияние оказывает постоянная k на форму фазовых траекторий и каков физический смысл этих изменений? Рассмотрите частный случай fe = 0. Каково дифференциальное уравнение системы в этом случае?

4.4. Для системы уравнений (О. Перрон)

х = X - 4у У\ху\; y=-y-\-AxV\xy\

Рис. 4.28. Структурная схема системы управления для примера 4.7

а) найти все положения равновесия;

б) построить фазовые траектории.

4.5. Проанализируйте введение корректирующего фильтра вида р - 1 для задачи управления положением искусственного спутника Земли, рассмотренной в § 4.1:

а) постройте линию переключения;

б) проанализируйте некоторые характерные фазовые траектории.

4.6. Существенное свойство системы, которое не рассматривалось при анализе движения искусственного спутника Земли в § 4.1, заключается в том, что наряду с точкой 6=0; в = О положением равновесия является любая точка 6 = 2tm; 6 = О (п = 1, . . .). Продумайте, как это свойство сказывается на результатах примера 4.1, п. 6. (У. Л. Нельсон).

4.7. Обратимся к системе, показанной на рис. 4.28. Найдите фазовый портрет в плоскости (е, е) (Р. Калман). .

См. сноску на стр. 77.

4.8. Оцените вид траекторий движения простого маятника j :+gsignj :=0 в нормальных координатах. Ответьте на следующие вопросы:

а) являются ли траектории системы одинаковыми во всем фазовом пространстве;

б) если вид траекторий различен, то каковы сепаратрисы системы; с) существует ли в системе предельный цикл?

4.9. Для системы, показанной на рис. 4.29, найдите фазовые траектории в нормальных координатах, если 0-<а<6-<с; fe>>0.

4.10. Для системы, удовлетворяющей условию = р2р q Р u=+U, где и - постоянная:

а) постройте фазовые портреты в нормальных координатах как для и = так и для и = -U; определите, каковы положения равновесия в каждом случае;

б) что происходит с вектором состояния (у, у) в момент t, когда управляющее воздействие переключается с и = +t/ на ы = -t/? Постройте характерную траекторию для случая, когда и (t) = -\-U при О <t<ii и и (i) = -U при t t;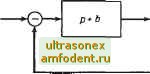

Рис. 4.29. Структурная схема системы управления для примера 4.9

в) выберите в качестве вектора состояния {Zy, Zg), где = у, такой вектор, чтобы уравнения системы в координатах (Zj, Zg) содержали лишь управляющий сигнал и (t), но не содержали его производной и (t) Для этих уравнений вновь выполните задания пунктов а) и б).

4.11. Для следующих систем первого порядка изобразите траектории системы как зависимость координаты X от времени t.

а) X = sin х;

б) х = sin х;

в) х-= х{х-\){х - 2);

г) =

(л; -2)2, 1

О в остальных точках. 4,12. Найдя уравнения фазовых траекторий в полярных координатах (г, 6), покажите, что системы

х = у+ х(х + у- \) sin

Л;2 у2 1 ,

у = -х + у {х+ у- \) sin

Л;2 + у2 1

имеют бесконечное число предельных циклов.

4.13. У консервативной системы л;/ (л;) = О определите выражение для касательной к траектории через координаты х к х.

4.14. Уравнение fix-\- tx-\-(fi - п) х = О известно как уравнение Бесселя. Определите:

а) является ли система линейной и автономной;

б) положения равновесия;

в) можно ли быстро построить фазовые траектории.

4.15. Для линейной системы х 2ах Ьх = О прикиньте в плоскости параметров а я b области устойчивости и неустойчивости положения равновесия. Проанализируйте виды положений равновесия для различных областей и на границах этих областей.

4.16. Рассмотрим военное сражение, когда каждая сторона успешно противостоит другой. В таких случаях скорость потерь каждой стороны пропорциональна числу солдат соответствующей стороны. Допустим, что число людей, участвующих в сражении, настолько велико

что может быть описано непрерывными переменными Ху и х. При этом переменные Xi и х удовлетворяют дифференциальным уравнениям Ланкастера

Xl = kiXyX, X2 212

Предлагаем читателю:

а) найти закон изменения Ху, при котором Х2 стремится к нулю, если > /гг и Xi, jCg > О при kik> 0;

б) найти положения равновесия и оценить их устойчивость, полагая, что Ху и могут стать отрицательными.

4.17. Для системы с обратной связью

w(0 =

1, е>2; О, I е I 2; -1, е<-2,

постройте траектории в координатах (е, е) и найдите положения равновесия. Проанализируйте их устойчивость.

4.10. УКАЗАНИЯ НА ЛИТЕРАТУРУ

Прекрасно написанная книга [3] оказала огромное влияние на развитие интереса к нелинейным системам. Она остается до сих пор одной из лучших книг, освещающих классические методы А. Пуанкаре и других исследователей. Главы 1-3, касающиеся фазовой плоскости и связанных с ней разделов, читаются очень легко. В книге приводится большое число примеров. Более современной является книга [30 j, которая также богата примерами.

К числу лучших книг по нелинейным системам, изданных до 1961 г., следует отнести книгу [63]. На стр. 315-345 и 370-393 этой книги рассмотрены чрезвычайно интересные примеры построения фазовых портретов для нелинейных систем второго порядка (не обязательно автономных). Читателю следует рекомендовать также книгу [112 ], в которой графическими методами анализируются системы третьего порядка. В этой книге содержится обширная библиография, включающая 735 работ по анализу нелинейных систем, выполненных до 1975 г.

Для желающих более глубоко ознакомиться с математической стороной вопроса рекомендуем гл. 2 книги [161 ], гл. 16 в работе [35] и гл. 2-4 книги [179] *.

* К числу интересных работ по применению метода фазовой плоскости и нелинейным дискретным самонастраивающимся системам, а также системам со случайными параметрами можно отнести монографии [281], [287] (Прим. ред.