применим теперь необходимые условия, развитые выше, к нелинейным системам. В этом случае в противоположность линейной системе примера 13.3 необходимые условия определяют двухточечную краевую задачу относительно 2п нелинейных дифференциальных уравнений.

Пример 13.4-). Динамику движения реактивного самолета, летящего в вертикальной плоскости, можно приближенно описать следующей системой дифференциальных уравнений первого порядка:

k(t)= v{t)cosy(f)=fx;

Д

z(t)= V (О sin V (О = f2,

Т COS a(t) -D Iv (t), a {t)] -

w(t) L Y(0 =

V it) w (t)

[T sm a (t) + L[v (t), a{t)]

wit) = -k = f

8 J

v{t)

- g siuyit) = fs;

cosY(0 = /-4;

(13.72)

где X {t) и z(i) v(i)

горизонтальное и вертикальное смещения самолета; величина вектора скорости самолета, направленной под углом у рад к горизонту;

Т - постоянная величина тяги, развиваемая реактивным двигателем; g - ускорение силы тяжести;

w - вес самолета; предполагается не зависящим от высоты г; D и L - соответственно лобовое сопротивление и подъемная сила, которые, в общем случае, являются функциями v и а; k - коэффициент, который характеризует потери веса из-за расхода топлива (рис, 13.5).

Найдем необходимые условия минимума времени полета, если в качестве управляющего воздействия использовать а (f). Иначе говоря, задача заключается в нахождении такой функции а (t), чтобы самолет, стартующий из точки с координатами (х, г) в момент времени / - О, мог достигнуть конечной точки (xg, Zg) за минимальное время t.

Как и в § 13.2, для удобства введем вспомогательную переменную ({):

ix(t) = a (t); II (0) = 0. (13.73)

Теперь можно определить шестимерный вектор x (f) с компонентами х (f), z (f), v (f), у (t), w it) яц (f). Ограничения, обусловленные дифференциальными уравнениями, представим в виде

ф1 = л; - fl, ф2 = г - /а; фз = г - /з = 0; Ф4 =т - / = 0; ф5 = ш-Ь А = 0.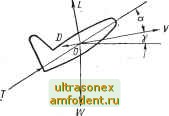

Рис. 13.5. Основные обозначения при полете реактивного самолета в вертикальной плоскости

Вводя множители яр (Q, . . ., ipj (f), образуем функцию

ii=i; ы()т{х,х).

Применяя метод множителей Лагранжа, преобразуем сформированную задачу в задачу нахождения вектора х (t) на интервале времени [О, tz], который минимизирует показатель

качества J {х, х, t) dt при отсутствии ограничений.

) См. работу [73]. М. X е с т и н с, очевидно, первым показал, что задачи оптимального быстродействия близки к рассматриваемой задаче Майера.

Необходимые условия существования минимума последнего функционала заключаются в следующем.

1. Уравнения Эйлер а- Лагранжа. Согласно уравнениям (13.63а) находим, что

1 (О = 0; 11)2 (О = 0;

Фз(0 = -ipiCoSY -ifa Sin Y + -

k + 8

дР {у, a)

--sm a ---(L - w cos y)

14(0 = ifif sin Y - ifai cos Y + ifsg cosY - 14 ~ sin y;

dL, g da w

Г cos a - D {v, a) +

+ 4-[Г sina + L(i>,a)];

Последнее уравнение аналогично соотнощению (13.476).

2. Условия Вейерщтрасса. Применяя уравнение (13.32), к настоящей задаче, получим

(13.75)

это означает, что оптимальный угол атаки а* {t) для всех t должен взбираться таким, чтобы

обеспечить максимум величины ifj (jc*, а). Так как только функции /з и /4 зависят от а,

условие Вейерщтрасса означает, что а следует выбирать, определяя максимум следующего выражения:

/г(у, a)iil)3(0--[rcosa-D(t>. a)]-fil)4(0-[rcosa-f L(t>, а)]. (13.76)

Если на величину а не иакладьшается ограничений, то необходимое условие Вейерщтрасса для этого случая принимает вид

]dh(v, а)

а=а*

= 0.

Г(13.77)

3. Условия трансверсальности. Для рассматриваемой задачи зафиксированы только значения х (fg) и z (fg) и, следовательно, 6x2 и dZg равны нулю. Кроме того, поскольку вариации 62 и 8x2 независимы, то коэффициенты при них должны стремиться к нулю; таким образом, из выражения (13.68) следует, что

% (2) =2 (2)=% (2)= О

\i=i

Так как функции не зависят явно от времени t, то 5

If*/* - 1 = О для всех tlO, у.

(13.78) (13.79)1)

(13.80)

1 Здесь fi=-fi {х\ а).

Чтобы получить решение задачи, необходимо решить 2п дифференциальных уравнений, составленных из соотношений (13.72) и (13.74) с учетом условий (13.77)-(13.80). Аналитическое решение задачи в этом случае найти нельзя, и поэтому необходимо обратиться К численным методам, которые рассмотрены в гл. 17.

13.4. ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ОБОБЩЕННЫМ ПОКАЗАТЕЛЕМ КАЧЕСТВА. ЗАДАЧА БОЛЬЦА

На основе вариационного исчисления оказалось возможным решить сравнительно широкий класс оптимальных задач управления. Наиболее общая постановка задачи заключается в следующем.

Рассмотрим системы вида

x = f{x,u,ty,x{t,) = x,. (13.81)

Требуется найти такую функцию управления и* (t) на интервале t t, которая, во-первых, переводит систему из начального состояния в конечное, для которого соблюдается следующее условие:

р 1х (t), t] = О, (13.82)

и, во вторых, обеспечивает минимум показателя качества

f = P\x {t), h\ + \L {x,u, t) dt. (13.83)

Наложим на функцию управления и ограничения вида ( ) = О, например, и? - = О, где k - постоянная.

Задача вариационного исчисления, в которой минимизируется обобщенный показатель качества (13.83) и присутствуют ограничения в виде системы

дифференциальных уравнений вида р {х, х, t) = О, называется задачей Больца. Она может быть сведена к задачам Лагранжа или Майера, хотя чаще ее удобнее решать, не прибегая к преобразованиям.

Оптимальное управление и (t), как правило, определяется способами, аналогичными изложенным выше. Если управление и имеет размерность г, то в начале образуем г вспомогательных переменным л; .1, . . ., Хп+г и г вспомогательных дифференциальных уравнений Xj = Ы/ {t); Xj {t = 0; У = n -j- 1, . . ., n + г; после этого получим

Z.2 (X, X, и, -ф, О = L\{x, и, О -f gt]); {t) (л:, x,u,t) +

-y.{t)Uu)L{x,x,u,i,t) + Ht)l{tt), (13.84)

гдеф,- xi - fi(x, и, t), i=l, ... n; ф,. - множители Лагранжа;

X - дополнительный множитель, обусловленный ограничениями, наложенными на и ();

1) Уравнения Эйлера - Лагранжа. Выписав уравнения

(-~- = О в явном виде, получим dxi dt \ dxi j

=--2! - = 0 /=Ь-..,г. (13.85)