рий не определено; в любой другой точке фазовой плоскости- оно определено однозначно. Тогда анализ поведения вблизи положений равновесия позволяет говорить о свойствах этого равновесного состояния. В следующем разделе мы проанализируем траектории линейных систем вблизи положения равновесия.

4.3. РАЗЛИЧНЫЕ ВИДЫ ПОЛОЖЕНИЙ РАВНОВЕСИЯ АВТОНОМНЫХ ЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА

Для линейных автономных систем, описываемых уравнением л: = Ах, фазовые координаты положения равновесия определяются из условия АХе = 0. Заметим, что решение х = О является единственным решением данного уравнения, когда определитель матрицы А не равен нулю. На основании этого получим следующую теорему.

Теорема 4.1. Начало координат линейной автономной системы х = Ах есть единственное положение равновесия при условии \ А\фО.

В частности, если все собственные значения матрицы системы отличны от нуля,) то начало координат - единственное положение равновесия (почему?). Если это так, то достаточно проанализировать траектории системы лишь в окрестности начала координат. Кроме того, в этом случае оказывается возможным, по крайней мере качественно, оценить характер траекторий системы на всей фазовой плоскости, анализируя их поведение вблизи начала координат.

Из последующего изложения будет ясно, что анализ траекторий линейных систем удобнее проводить при описании их в канонической форме, поскольку при таком представлении каждая составляющая общего движения определяется одним из собственных значений. Однако, как правило, в качестве фазовых координат выбираются выходная координата системы у и ее скорость у, что соответствует нормальной форме записи уравнений системы. Связь между нормальной и канонической формами записи определяется линейным преобразованием * (в частном случае, когда все к - различные корни, матрицей преобразования является матрица Вандермонда, как это было показано в гл. 3). Кроме того, начало координат в нормальных фазовых координатах соответствует началу координат в канонических фазовых координатах. Естественно ожидать, что основные черты поведения фазовых траекторий вблизиначала координат сохраняются при переходе от одной системы координат к другой; при этом изменяется лишь форма кривых. Тогда без ограничения общности, можно изучать траектории системы лишь в канонической системе координат. Уравнения системы второго порядка с различными полюсами в канонической форме запишем в виде

xi = -ii; xi (0) = xio;

X2 - 2X2, X2 (0) = X20. I

Решение системы (4.21) очевидно и равно

Xl{t) = xt, X2{t) = X2f. (4.22)

Случай 1. Оба собственных значения не равны нулю и представляют собой действительные числа одного знака. Из уравнений (4.21) следует

(4.21)

dXi %х

(4.23)

* В общем случае это преобразование не будет ортогональным и, следовательно, не эквивалентно простому повороту осей (см. приложение I).

откуда найдем

Х2 = CXj ,

(4.24)

где с - произвольная постоянная.

Уравнение (4.24) определяет вид фазовых траекторий, которые изображены на рис. 4.12, а для случая <;Я,2 < О, а на рис. 4.12, б - для случая Я,2 < Я,1 < 0.

Положения равновесия в начале координат, как они показаны на рис. 4.12, называются узловыми точками (узлами). Это устойчивые узлы, так как собственные числа Я <2 0 (г = 1, 2). Если же собственные числа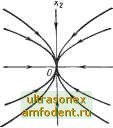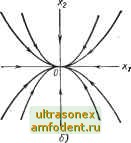

Рис. 4.12. Вид фазовых траекторий в канонических координатах для системы второго порядка, имеющей собственные значения и к:

а г- при Я, < Яг < 0; б - при Яг < Яг < О

Рис. 4.13. Вид фазовых траекторий в канонических координатах для системы второго порядка, имеющей собственные значения, удовлетворяющие условию

K<o<iK

положительны, то узлы неустойчивы, и хотя вид фазовых траекторий сохраняется, однако движение по ним направлено в противоположную сторону.

Случай 2. Оба собственных значения не равны нулю - действительные числа разных знаков. Из уравнений (4.22) или (4.24) для этого случая следует, что фазовый портрет имеет вид, показанный на рис. 4.13. Такой тип положения равновесия называется седловой точкой. Этим отмечается тот факт, что всякое движение, приближающееся к этой точке, в конце концов направлено от нее. Нет необходимости дополнительно пояснять, что седловая точка неустойчива.

Случай 3. Собственные значения - комплексно-сопряженные числа. Если использовать каноническую форму записи уравнений, то получим

Xl = (а -f ур) Xl, Ха = (а - /р) х. (4.25)

Эти уравнения имеют следующие решения:

Xl = Xioe *e/P* = Xioe * (cos -f / sin p);

= X2oe *e-P* = X2oe * (cos pt - j sin pt).

Таким образом, канонические координаты х и Xg комплексно-сопряженные. Поскольку координаты - комплексные числа, то изобразить фазовый портрет, оказывается, достаточно сложно. Поэтому целесообразно выполнить следующее преобразование.

Пусть

Xi - 1 4 12, Х2 - 2 - JZ

(4.26)

где числа и предполагаются действительными. Определяя их по соотношениям (4.26), получим

= 4 + 2) = cos t; 22 = (Хг - X2) = -z sin

(4.27)

Вводя плоскость комплексного переменного с координатами и /Zg, мы приходим к выводу, что решение

хх (О = 1 it) + /2 () = Xioe e/P;

; Jl (0) = Xio = + /220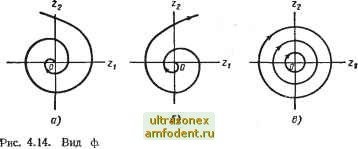

азовых траекторий для системы, описываемой уравнениями (4.27):

при а < 0; б - при а > 0; в - при а = О

определяет в этих координатах логарифмическую спираль. Если а <<0, то движение по спирали будет направлено к началу координат, а фазовый портрет имеет вид, показанный на рис. 4.14, а. Если а > О, то движение по спирали направлено от начала координат (рис. 4.14, 6). Если а = О, то фазовые траектории являются замкнутыми кривыми с центром в начале координат, как показано на рис. 4.14, в.

Положение равновесия при а < О называется устойчивым фокусом, при а > О - неустойчивым фокусом, а при а = О - центром.

Когда а = О, движение в системе периодическое, а его период одинаков по любой траектории и равен 2эх/р.

С л у ч а й 4. Ненулевые кратные полюсы. Как уже говорилось в гл. 2, для этого случая матрицу А необходимо записать в жордановой канонической форме. В этом случае движение в системе удовлетворяет уравнению

(4.28)

где k - постоянная величина, возможно равная нулю. Тогда решение имеет вид

x{t) = kx2je + Xi*; X2(t) = X2 . (4.29)