Поставим следующие вопросы:

1. Каково среднее значение выходного сигнала у (() системы в установившемся состоянии, если входной сигнал постоянен и равен Ю

2. Сколь быстро будет отслеживать система ступенчатый входной сигнал г (t), если t/ = 2, В = 10 сек--2, 6 = 25 сек и а = 1 сек~.

3. Каковы преимущества и недостатки этого типа автоколебательного сервомеханизма по сравнению с обычным сервомеханизмом, где реле заменяется линейным усилителем с коэффициентом k и имеюпщм насыщение при и= ±U? Допустим, что усиление k таково, что замкнутая система устойчива, а ее относительный коэффициент демпфирования равен g = 0,48.

Решение. 1. В силу интегрирующих свойств линейного элемента сигнал е на входе линейного элемента имеет нулевое среднее значение. Это означает, что в установившемся состоянии среднее значение у (f) равно R.

Составляющая / сигнала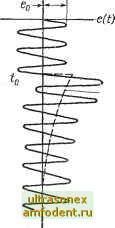

- Составляющая сигнала

Рис. 7.11. Иллюстрация переходных процессов в колебательной сервосистеме (рис. 7.10), когда на нее действует малая по уровню команда управления

2. Пусть входные сигналы (см. рис. 7.10) имеют следующий вид: г (О = t< U; г (t) = i?o + t> t.

(7.46)

Предположим, что при t= Iq система находится в установившемся состоянии: ее выходной сигнал у имеет среднюю величину у = R а сигнал на входе реле в среднем равен нулю.

Далее при t= to входной сигнал изменяется скачком на R. Пусть - амплитуда автоколебаний на выходе, тогда сначала рассмотрим случай малых ступенчатых изменений

входного сигнала ] К е. Из рис. 7.11 можно заметить, что переходный процесс от прежнего равновесного состояния (средняя величина у = Ro при to) стремится к новому положению равновесия (средняя величина y=Ro-i- Ri)- Последнее связано с непрерывным периодическим переключением реле. Можно ожидать, что время перехода будет порядка величины периода автоколебаний.

Рассмотрим случай \Ri\ (см. рис. 7.10). Если Ri1> О, то е {t) будет оставаться -больше нуля до тех пор, пока у не увеличится настолько, чтобы свести сигнал е до нуля. В этот

момент вновь возникают колебания. Теперь положим R > е,; тогда время переходного процесса будет приблизительно равно времени, в течение которого выход линейного объекта изменяется от величины Rg до R, + Ri, когда на входе линейного объекта сигнал равен U. Приближенно переходный процесс описывается функцией

(7.47)

(7.48)

У ih) Rb+ Ri. Ri > e ,

где tl - время протекания переходного процесса.

С учетом численных значений параметров уравнения (7.47) принимают вид

y(t- to) Ro+ 20,8 le- it-u) 1 ] + 20 (if - to); 1 y(ti)Ro+Ri; totto+ti. 1

Амплитуда автоколебаний приближенно равна во 1,0.

Рассмотрим теперь ступенчатое изменение сигнала, большее чем во, например Ri = 8; тогда по уравнению (7.48) определим /i = 1,1 сек.

Переходный процесс в рассматриваемой, системе при ступенчатом изменении сигнала Ri= 8 был получен на аналоговой вычислительной машине [кривая yi(t), рис. 7.12, а]. До того момента, когда на систему был подан ступенчатый входной сигнал, в системе имели место устойчивые автоколебания. Рис. 7.12, а позволит определить ряд характеристик системы, которые приведены в табл. 7.1.

Таблица 7.1

Сравнение измеренных и вычисленных величин для примера 7.4

3. Возможность управления объектом зависит от имеющейся мощности. Следовательно, когда сравнивается работа различных типов сервомеханизмов при одном и том же объекте, важно, чтобы предельное значение управляющего воздействия сохранялось одним и тем же. В нашей задаче величина управления и ограничена уровнем ±U.

Для линейных сервомеханизмов с насыщением по уровню ± U коэффициент усиления k можно выбрать таким, чтобы при работе на линейном участке система бьша устойчивой и имела приемлемое затухание. Характеристическое уравнение при работе в линейной зоне равно р2 + [а - {kB/b)]р + kB=0, или

р2+2со р-Ьсо2 = 0,

(7.49)

со = YkB ; I --

2со

2 YkB,

:(7.50)

Пусть ft = 0,1, в = 10 сек-2, а со = 1 се/с и g = 0,48. Эта система была также промоделирована на аналоговой вычислительной машине. Переходный процесс при ступенчатом изменении Ri= 8 описывается кривой у (t) (см. рис. 7.12, а).

Сравнивая характеристики переходного процесса колебательного сервомеханизма yi (i) и линейной системы уЫ (см. рис. 7.12, а), отметим, что переходный процесс в линейной системе имеет большую длительность, нежели в автоколебательном сервомеханизме. Причина

этого заключается в том, что колебательный сервомеханизм использует всю мощность управления. Линейный сервомеханизм с насыщением не использует в полной мере имеющуюся мощность.

Теперь рассмотрим некоторые адаптивные свойства колебательного сервомеханизма. В реальных условиях параметры объекта управления могут изменяться в широких пределах, причем закон изменения их может быть и неизвестен. Типичным примером такового поведения

гт W

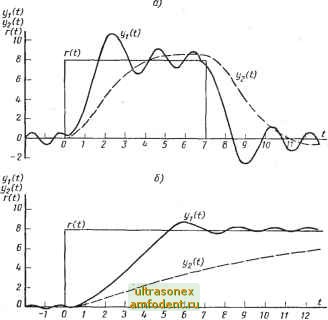Рис. 7.12. Переходные процессы в колебательной у, (t) и линейной у2 if) сервосистеме (пример 7.4) при действии ступенчатого входного сигнала: а - при В - 1й сек ; б - при В = 5 сек ; е - при В = 1 сек

является полет ракеты при изменяющихся условиях внешней среды. Причем, когда проектируется линейное управляющее устройство с учетом ограничения управляющего воздействия, нужно сначала определить возможные диапазоны изменения параметров объекта, а затем пайти такое усиление управляющего устройства, которое обеспечивает устойчивую работу всей системы.

На рис. 7.12, б, в показаны переходные процессы в системе при коэффициентах объекта усиления В = 5 сект и В = 1 сек~. При этом видно, что переходный процесс при автоколебательном сервомеханизме протекает значительно быстрее, чем при линейном. В автоколебательных системах независимо от величины параметров объекта управления эквивалентный