x = xs!ncjt

ll(X,CJ)\ = X

uusin(cjt+0)

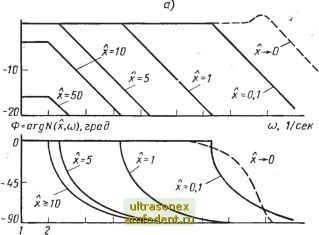5 70 20 50 WD 200 500 WOO

cj, 1/сек

Рис. 6.21. Нелинейный привод:

а - структурная схема; б - амплитудная и фазовая характеристики нелинейного привода, полученные по его эквивалентной передаточной функции

ImNG(ju)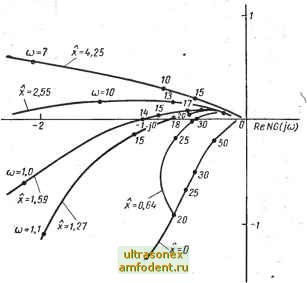

Рис. 6.22. Амплитудно-фазовые кривые (годографы) N (х, со) G (/со) при ряде значений х (для примера 6.9)

Возможный вид корректирующего звена можно определить так:

Gi (Р) = 10.53

(6.67)

В этом случае передаточная функция линейной части разомкнутого контура всей системы задается соотношением

G (s) = Gp {S) Gi {S). :

С учетом эквивалентной передаточной функции нелинейного привода годограф частотной

характеристики всего разомкнутого контура N {х, со) G (/со) показан на рис. 6.22. Из рисунка

видно, что для малых амплитуд х система-удовлетворительна. Однако при увеличении ампли-

туды X наблюдается резкое ухудшение качества системы. Действительно, при х= 1,6 и соо = = 14 1/сек в системе возникают неустойчивые автоколебания. Таким образом, метод гармонической линеаризации позволяет заключить, что система, устойчивая при малых сигналах, становится неустойчивой, когда амплитуда сигнала возрастает.

Из, возможных способов устранения неустойчивости указанного типа рассмотрим следующие:

1. Необходимо уменьшить коэффициент усиления разомкнутого контура настолько, чтобы

частотный годограф для всехх пересекал отрицательную часть действительной оси справа от точки -1; /О (см. рис. 6.22).

2. Спроектировать линейный фильтр, который позволяет достичь тех же результатов.

3. Ввести в контур нелинейный элемент с характеристикой тцпа ограничение для того,

чтобы амплитуда х не превышала критической. ,

Рассмотрение годографа (см. рис. 6.22) показывает, что способы 1) и 2) позволяют стабилизировать систему управления, но в ущерб качеству и точности переходных процессов при малых сигналах. Способ же 3) или комбинация 1) и 3) могут дать простой и эффективный метод стабилизации при. сохранении удовлетворительного качества системы и при малых сигналах. Лучше всего это пояснить исходя из понятия запаса по амплитуде для нелинейной системы. Напомним, что для линейных систем с обратной связью эффективность того или иного способа обеспечения устойчивости определяется запасом устойчивости по амплитуде, который определяет диапазон возможного увеличения усиления разомкнутого контура, приводящего к неустойчивости замкнутой системы. Это позволяет определить запас устойчивости по амплитуде и в нелинейной системе как такую величину усиления, которая приводит к возникновению автоколебаний в замкнутой системе при заданной амплитуде в некоторой точке системы *. Для рассматриваемой системы запас по амплитуде Кс может быть получен из годографа

частотной характеристики (см. рис. 6.22). Для заданной амплитуды х запас Кс есть величина

j---, определяемая на той частоте, где фазовая характеристика

I Na (х, соо) Gi (/соо) Gp (/Мо)

разомкнутого контура пересекает уровень -180°, т. е.

.. Кс{) =--!-, . , , (6.68а)

I Na {X, соо) Gi (/соо) Gp (j) \

где шо определяется условием .

arg [Na (х, мо) (/шо) Gp ( мо)] = -180°. (6.686

Результаты расчета представлены на рис. 6.23, где показана зависимость запаса по амплитуде в нелинейной системе Кс = Кс (х) как функция амплитудь! х. Здесь также указаны значения частоты Шо, где фазовый сдвиг частотной характеристики разомкнутого контура равен -180°. Отметим, что для х 1,6 запас по амплитуде в децибелах становится отрицательной величиной, что и определяет неустойчивость для больших сигналов.

* Определение запаса устойчивости по амплитуде в нелинейной системе безусловна основано на том же предположении, ioropoe лежит в основе интерпретации понятия устойчивости в методе гармонической линеаризации.

Используя рис. 6.23, можно получить кривые, определяющие запас устойчивости по амплитуде в нелинейной системе в зависимости от амплитуды других сигналов. Например,

интересно построить такую зависимость от амплитуды у выходного сигнала. Соотношенне

между X к у задается выражением

y = \NA (х, с) GpI =

(6.69)

Kc{x)\Gi{m)\

где Gi (р) определяется по (6.67). Кривая Кс = Кс (у), показанная на рис. 6.24, может быть таким образом получена из кривой Кс= Кс(х) (см. рис. 6.23).

20 10 О

-20 -3D

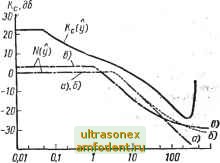WOO у

5 ID 20 50 100 X Рис. 6.24. Запасы устойчивости Кс и эквивалентный коэффициент передачи для нелиней-Рис. 6.23. Запасы устойчивости нелинейной ного корректирующего устройства в зависи-

0,05 0,1 0,2 0,5 1

яс. 6.23. Запас! системы Кс (х) по амплитуде для примера 6.9

мости от амплитуды выходного сигнала у

Теперь можно стабилизировать систему, преобразуя сигнал ошибки нелинейным звеном. Структурная схема системы с нелинейной компенсацией показана на рис. 6.25. Влияние нелинейной коррекции е = f (е можно проанализировать, изображая эквивалентный коэффициент передачи N (ej = N (у) вместе с кривой Кс {у) Для системы без нелинейной коррекции

Рис. 6.25. Структурная схема системы управления с нелинейным корректирующим устройством:

1 - нелинейное корректирующее устройство; 2 - прямая цепь структурной схемы (рнс. 6.20)

на рис. 6.26. Поскольку кривая Кс (у) указывает, на сколько можно увеличить коэффициент усиления в системе без нелинейности / (е), чтобы не возникли колебания, то нелинейный элемент должен вызвать уменьшение запаса по амплитуде с ростом его эквивалентного усиления.

Таким образом, как показано на рис. 6.26, запас устойчивости по амплитуде с нелинейностью / (gj) задается выражением

К (и) дб = fc(y) дб - N {у) вб>

(6.70)