4. Дельта-метод

Этот метод наиболее приспособлен для получения отдельной траекто-. рии. Пусть система описывается уравнениями вида

Xi =. х; = -/ {xi, х). (4.43)

Добавляя и вычитая во втором уравнении величину cooXi, получим

Xi= Х2, х2 = -alxi - 6 {х, х).

б (Xi, Ха) = f (Xi, Xs )- oilx:

(4.44)

(4.45)

Снова предполагаем, что б (х, х) постоянна в малой окрестности точки {Xi, Xj) на фазовой плоскости, тогда

cjoX,

(4.46)

и при интегрировании получим (с условием, что 6 - постоянная величина)

-g- Л--2 + 1

Это уравнение можно представить в виде

Рис. 4.25. Построение фазового портрета с помощью дельта-метода

б (Xi.Xa)

= i? (4.47)

Данное соотношение означает, что малый участок траектории вблизи точки (cooXi, Xg) можно заменить дугой окружности радиуса R с центром в точке

б (Xi, Ха) р

если в качестве фазовых координат принять координаты (WoXi, Xg). Построения, связанные с дельта-методом, приведены на рис. 4.25.

5. Метод Пелла

Метод Пелла * [157] целесообразно использовать для построения отдельных траекторий автономных систем второго порядка, которые можно описать уравнением вида ** х + g (х) + / (х) = 0. Для этого класса систем, полагая Xi = х, Ха = х, получим

Ас2 ~gte) - / (%) dxy % *

И в этом случае цель остается прежней: отыскать наклон в заданной точке (Xj, Ха). После того как построен малый orpesfOK с заданным наклоном,

* В отечественной литературе этот метод чаще называют методом Льенара (Прим. ред.). ** Этот метод можно развить и на системы более общего вида. См., например, работы [166] и [195].

(4.48)

аппроксимация траектории в этой точке заканчивается, и следует перейти к следующей точке.

Для нахождения воспользуемся следующим приемом:

1. Используем отрицательную полуось для построения кривой g (х), а отрицательную полуось для построения / (xj), как это показано на рис. 4.26.

2. Из произвольной точки плоскости (а, Ь) опустим на оси х и Ха перпендикуляры и продлим их до пересечения с кривыми g (Ха) и / (Xi), как показано на рис. 4.26.

3. Откладываем отрезок длиной \[{а)\ вдоль оси Xl из точки а в отрицательном направлении, если ордината / (а) положительна, и наоборот. Получим точку С.

4. Из точки С откладываем отрезок длиной \ g {Ь)\ также вдоль оси Xi в отрицательном направлении, если ордината g (b) положительна, и наоборот. Получим точку D.

5. Точку D соединяем прямой линией с точкой {а, Ь). Маленький отрезок перпендикуляра к проведенной прямой в точке (а, Ъ) и является участком касательной к искомой траектории.

Обоснование этого построения заключается в том, что прямая, соединяющая точку D с точкой (а, Ь), имеет наклон . - Тогда отрезок

прямой, перпендикулярный к проведенной линии, имеет отрицательный наклон и точно соответствует правой части уравнения (4.48).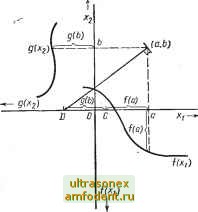

Рис. 4.26. Построение фазового портрета по методу Пелла

4.7. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ПРОТЕКАНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ФАЗОВЫМ ТРАЕКТОРИЯМ

Поскольку в основу построения фазовых траекторий заложена идея исключения времени, то после того как они построены, возникает задача восстановить временные характеристики процесса. Рассмотрим три метода, приемлемые для систем вида

X = / (X, к). (4.49)

1. Интегрирование выражения

- dx==ti - to-

(4.50)

Это условие достаточно очевидно, и его графическая интерпретация показана на рис. 4.27, а.

2. Интегрирование выражения вида

J f {x, x) J dx

(4.51)

Графически это означает, что мы определяем площадь под кривой

f (X.. X)

как это показано на рис. 4.27, б.

3. Можно выполнить построения, исходя из графического изображения траекторий. В основе этих построений лежит дельта-метод. Смысл метода заключается в том [см. уравнение (4.44)], что для малой дуги, проведенной

вдоль траектории из точки -

мы получим

X + (ogx + б = 0:

(4.52)

Тогда на отрезке дуги в угле 6 скорость перемещения фазовой точки, как это следует из интегрирования (4.52), приближенно определяется как

Площадь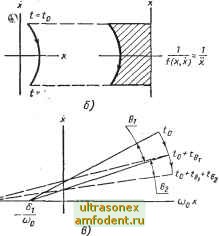

Площадь

Рис. 4.27. Графическое определение времени протекания переходного процесса по фазовым траекториям, построенным в координатах (х, х):

а - на основе уравнения (4.50); б - на основе уравнения (4.51); в - с использованием соотношения (4.52)

(i)(,t. И для малых углов 6 справедливо (0о4 = 6; поэтому L = -, где 4 ~

Приближенная оценка времени, необходимого для движения по дуге О (рис. 4.27, в).

Если траекторию можно разбить на m дуг с углами 6, Gg, . . ., (рис. 4.27, в), то ясно, что полное время движения по такой траектории равно

4.8. КРАТКОЕ СОДЕРЖАНИЕ

Практически любые стационарные системы второго порядка можно с успехом анализировать на фазовой плоскости. В процессе многолетней практики было разработано большое число методов построения фазовых траекторий и способов анализа таких систем.