в выпуклое множество О (t) ) (см. рис. 14.2а). В пределе при т. е. к минимальному времени, мы все еще будем иметь

{ц>.х(и,О){фх{0)). (14.9)

Теперь, с учетом соотношения х ( *, t*) = х (0), получим

(г,1.л: {и, О) {и. О), [(14.10)

где, как следует из сказанного выше, rj* является вектором внешней нормали к опорной плоскости выпуклого множества (3 (/*) в точке х (0) (рис. 14.2, б). В дальнейшем вектор rj<* будем обозначать как rj.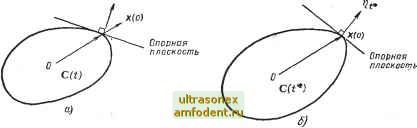

Рис. 14.2:

а - достижимое множество С W, которое не содержит точки х (0); б - достижимое множество С (О, Для которого точка X (0) принадлежит границе

Из сотношений (14.10) и (14.4) следует важный вывод о том, что оптимальным по быстродействию является такое управление и (f), которое доставляет максимум выражению

SJ~ SM/()- (14. И)

1=1 о /=1

После изменения порядка суммирования и интегрирования уравнение (14.11) принимает вид

п f / п \

212 ncbije-

j=10 \t=l

мДт)т,

(14.12)

и достигает максимума только в том случае, когда

и] (т) = sign

/= 1, n.

и* (т) = sign [tfe--B].

( 14.13)

Таким образом, всякий раз, когда ни одна из составляющих вектора g (т) А {цте-лхВУ не равна тождественно нулю в течение некоторого конечного отрезка времени, управление и* (т) является релейным.

Теперь видно, что каждая составляющая векторной функции g (t) является линейной комбинацией п затухающих экспонент. Тогда в соответ-

Читатель может сам убедиться в том, что через каждую точку на границе выпуклого множества всегда можно провести, по меньшей мере, одну опорную плоскость, которая, согласно определению, располагается таким образом, что все выпуклое множество целиком лежит по одну сторону этой плоскости. Внешняя нормаль направлена к той стороне опорной плоскости, которая не содержит точек выпуклого множества.

ствии с результатом, известным иногда под названием правила Декарта, каждая составляющая g {%) может иметь самое большее п-1 действительных нулей ). Таким образом, каждая компонента управления и] (f) имеет самое большее п-1 переключений.

Таким образом, нами доказаны две важные гипотезы относительно задач оптимального быстродействия, о которых сказано в гл. 12, а именно: гипотеза о релейности управления и теорема об п-1 переключении применительно к линейному объекту управления с действительными собственными значениями. Эти положения были легко доказаны с использованием геометрических представлений. Но в то же время заметим, что рассматриваемая в данном параграфе система имеет существенные ограничения. В частности, предполагается, что управление и {}) является п-мерным, а матрица В - не особой. Это условие нарушается, например, для простейшей системы управления, в которой существует единственная функция управления объектом п-го порядка. И, наконец, заметим, что данный метод применим лишь к системе п-го порядка с отрицательными различными действительными корнями.

Ж.Ла-Саллю [117] удалось продвинуться дальше и снять ряд ограничений, рассмотрев аспекты управляемости и единственности решений.

14.2. ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЕ ЛИНЕЙНОЙ СИСТЕМОЙ

В предыдущем параграфе предположение о том, что матрица В размерности п хп не особая, необходимо лишь для доказательства существования допустимого решения. Если от этого ограничения отказаться в надежде на то, что существование функций управления будет доказано кахими-либо другими средствами, можно получить более общие результаты относительно решения задач оптимального быстродействия для линейных систем [117].

Рассмотрим произвольную стационарную линейную систему п-го порядка.

х = Ах + Ви, л:(0) = л-о,

где В - произвольная матрица с постоянными коэффициентами размерности ПХГ, а \Uj (011, / = 1, . . ., г. Для канонической формы матрицы А по аналогии с уравнением (14.4) имеем

- X, (0) = J е V 2 bijUj (т) Л, t = 1,.. ., п. (14.14)

о 7=1

Опустив вопрос о существовании допустимого управления, можно пока-.зать, что достижимое множество G (t) в данном случае является выпуклым. Более того, выпуклость множества G (t) можно доказать даже для нестационарной системы. При этом множество G (t) должно быть замкнутым.

Ла-Салль изучал оптимальное по быстродействию управление произ-Больной нестационарной линейной системой вида

х = А (t)x + B(t)u, х{0) = Хо, (14.15)

где В (t) - произвольная матрица размерностью п хг. Один из основных вкладов, внесенных Ла-Саллем, состоит в доказательстве того, что G (t) .даже для нестационарной линейной системы является не только выпуклым,

) Доказательство методом ивдукции см. в работе [162], стр. 122. .

но и замкнутым. Кроме того, он показал, что достижимое множество системы с релейным управлением и (t) в точности то же, что и в случае, когда и (t) просто отвечают ограничению Му () 1, / = 1, . . ., г.

Используя эти результаты, докажем следующие теоремы.

Теорема 14.1. Если из всех релейных кусочно-непрерывных управлений ) для системы (14.15) имеется одно, которое переводит изображающую точку из положения х в начало координат за минимальное время, то это есть оптимальное по быстродействию управление.

Теорема 14.2. Если оптимальное по быстродействию управление существует, то всегда найдется кусочно-непрерывное релейное управление, которое является оптимальным. Более того, все оптимальные управления имеют форму

и* (f) = sign [г1ф-1 {t, 0) В (t)r, (14.16)

где т) -п-мерный вектор, тождественно не равный нулевому.

Геометрически rj снова представляет внешнюю нормаль к опорной плоскости выпуклого достижимого множества G (f) в точке х (0).

Рассмотрим вопросы существования и единственности решений. Оказывается, на вопрос о единственности решений можно ответить с большей степенью общности, чем на вопрос о существовании решений.

Заметим, что если ни одна из п составляющих величины [тФ- {t, 0) х X В {f)] не обращается в нуль в течение конечного интервала времени при г\ =h О, то оптимальное управление и * {f) можно однозначно определить с помощью соотношения (14.16). Подобные системы будем называть управляемыми в смысле Ла-Салля, или L-управляемыми ).

Полезно рассмотреть стационарные L-управляемые системы. В этом случае необходимо, чтобы при rj = О ни одна составляющая rj e-Р тождественно не равнялась нулю. Последнее утверждение полностью эквивалентно тому условию, что на каждую переменную системы может непосредственно воздействовать каждая составляющая функции управления. Это более жесткое требование по сравнению с требованием полной управляемости гл. 3. Напомним, что полностью управляемая стационарная система обладает тем свойством, что на каждую переменнукз системы может непосредственно воздействовать, по меньшей мере, одна составляющая функции управления. Это эквивалентно требованию, чтобы не все п составляющих вектора [цФ- {t, G) В {t)] были равны нулю. Полной управляемости недостаточно для гарантии единственности оптимального по быстродействию управления. Этот вопрос более подробно рассмотрен в гл. 16.

Можно отметить, что линейная полностью управляемая система с одним входом (/ = 1) также L-управляема. Таким образом, если для некоторой линейной, полностью управляемой системы с одним входом существует оптимальное по быстродействию управление, то оно единственно.

Что касается вопроса о существовании решений, то единственный важный результат, о котором можно упомянуть, касается систем с линейными стационарными объектами управления. Ла-Салль доказал, что для этого класса систем всегда существуют оптимальные по быстродействию решения, если объекты управления устойчивы и полностью управляемы, как об этом уже было сказано гл. 12.

1) Здесь приводятся результаты Ла-Салля, развитые далее Галкиным; см. [68].

) Ла-Салль этот тип систем называет нормальным. Так как в данной работе используются термины, отличные от принятых в вариационном исчислении, мы предпочитаем не придерживаться указанной терминологии.