откуда йидно, что с исчезновением заключенной в квадратные скобки величины в приведенных выше уравнениях при конечном значении г]) имеем 2ах = 0; 2Ьх2 = О, т. е. получается неприемлемое решение, так как оно не удовлетворяет ограничению. Далее, если г]) = оо, то второй член каждого уравнения (16.3) становится неопределенным и х* найти невозможно.

Однако очевидно, что поставленная здесь задача все же имеет решение Xj = \; Х2= О 2 = 0; = l), в чем читатель может убедиться путем непосредственной подстановки. Для предотвращения возможности появления равенства (16.2) можно ввести два множителя Лагранжа я]Зо и и образовать величину

h {х Х2) = !])(,/ (%, Х2) + ig (xi, Х2). (16.4)

Если теперь выполнить действия, указанные в условии (16.1), даже когда g удовлетворяет соотношению (16.2), то эту задачу все же можно решить при фо = 0.

В общем случае минимизации функции п переменных / (хц . . ., а: ) с ограничениями gi (х, . . ., х ), (i = 1, . . ., т; п т) образуем сначала

h (х) == ijjo/ + Zj Фг§1- Можно показать [65], что если в точке минимума л:* t=i

ранг матрицы Idgildx,] размерностью пхт меньше т и если вектор df/dx не равен нулю в точке л:*, то тогда iJjo = О представляет собой необходимое условие существования т множителей ф . . ., ij;, не все из которых равны нулю и удовлетворяющих условию

Случай, в котором i5o = О, будем называть особым. Такого рода задача оптимального управления представляет собой аналог вырожденного случая в] вариационном исчислении.

Рассмотрим функцию Гамильтона для типичной задачи оптимального управления

. H%L-\-iff = %L + Н. (16.5)

Предположим, что существует такая задача, что оптимальная траектория л:* (/) и оптимальное управление к* (/) удовлетворяют всем необходимым условиям для приведенной функции Гамильтона Н = ч]: /. Тогда для того, чтобы гамильтониан (16.5) дал также оптимальное решение, должно быть выполнено условие i5o = 0. Оптимальная траектория л:* (t), вдоль которой фо = О, называется особой оптимальной траекторией. Задачу управления, дающую особую оптимальную траекторию, будем называть особой задачей оптимального управления.

Возможным примером особых задач управления являются задачи, в которых решение не зависит от функции L. Этот класс задач плохо сформулирован, так как на решение не будет оказывать влияние показатель качества j. Однако из этого случая можно получить некоторые геометрические указания, которые могут быть полезны при рассмотрении других вырожденных и особых задач управления.

Отметим, что lo будут тождественно равняться нулю, если достижимое множество G в конечной точке в п -f 1-мерном пространстве таково, что ось Xо параллельна опорной плоскости к (3 в этой конечной точке. В подобном случае вектор i]5, который, как было показано, перпендикулярен извне к достижимому множеству G, будет тогда иметь составляющую о, равную нулю.

Для иллюстрации сказанного выше рассмотрим следующий пример.

Пример 16.2. Пусть имеем систему первого порядка функцию управления и* (() в интервале времени [О, 1

X = и. Желательно найти такую с учетом О (t) :szl, которая пере-

водит состояние системы из л; (0) = О в л; (I) = 1, максимизируя вместе с тем критерий качества

Так как /= -min (-/), то приведенную выше задачу можно решить также путем минимизации J - - и (f) dt с последующим изменением знака найденного критерия

оптимальности на обратный.

Эта задача сформулирована недостаточно хорошо, так как имеется лишь одна функция управления, а именно: и {t) = 1, которая может переместить л; (О из О в 1 за отведенный интервал времени, следовательно, и* (t) = 1. Теперь можно показать, что в данной задаче iJ)o должна-равняться нулю, чтобы принцип максимума был удовлетворен.

Гамильтониан для нашей задачи имеет вид

ЯСфо, X, и. 0 = -Фо Vl~u(t) +iu{t). (16.6)

Таким образом, в соответствии с принципом максимума имеем

Н* (О = Н(о, 1, X*, и*, t) >Цао, 1, х\ и, t). При и* (t) = 1 выражение (16.6) принимает вид ф1-оК 1- (0 + % (0- (16.7)

Рис. 16.1. Достижимое множество системы, рассматриваемой в примере 16.2

Это условие должно быть удовлетворено для всех допустимых ы (О-

Так как дН/дх = О, то является постоянной. Напомним, что в соответствии с принципом максимума ч); также является постоянной с неположительным значением, а г])о и не могут равняться нулю одновременно. Если ipg .= О, то уравнение (16.7) может быть выполнено при положительном значении ipi- Однако, если iJJq < О, то нельзя найти ip, которая удовлетворила бы уравнению (16.7) для всех допустимых и (t). Таким образом, мы видим, что я]Зо = О представляет собой единственное решение, и потому оно является особым.

Тот факт, что iJJq равно нулю, можно определить также путем рассмотрения достижимого-множества для данной задачи. При Хд = f читатель может сам убедиться в том, что достижимое множество в зависимости от Xq и х, принимает вид области, изображенной на рис. 16.1. В точке X = Хх внешняя нормаль достижимого множества должна располагаться вдоль оси х,; следовательно, iJjq = 0.

Конечно, особые задачи управления не обязательно бывают такими наглядными, как в примере 16.2, но очевидно, что нетривиальные особые задачи управления серьезно еще не изучались.

16.2. ВЫРОЖДЕННЫЕ УПРАВЛЕНИЯ В ЗАДАЧЕ ОПТИМАЛЬНОГО БЫСТРОДЕЙСТВИЯ

В задачах оптимального управления траектория считается особой, если вдоль нее небходимые условия оптимальности, обеспечивающиеся принципом максимума, удовлетворяются нетривиальным образом. В этих случаях, несмотря на использование обычных необходимых условий, не удается получить полезной информации. Для нахождения оптимальной траектории приходится тогда применять другие методы. Задачу оптимального управления, в которой находят оптимальную вырожденную траекторию, будем называть вырожденной задачей оптимального управления.

В случае оптимального по быстродействию управления линейным стационарным объектом единственным проявлением вырожденного управления

* Предполагается, что в данной задаче следует использовать положительное значение квадратного корня.

является неединственность управления и* (t). Последнее было отмечено в гл. 14, а теперь рассмотрим это более детально.,

В гл. 14 было показано, что для задач оптимального по быстродействию управления линейным объектом при ограничении \ и {f) \ = U в соответствии с принципом максимума оптимальное управление должно быть представлено в виде

Если i-я строка матрицы представлена вектором-строкой bi (т. е. bt представляет собой 1-й вектор-столбец В), то мы имеем

иI {t) = и sign [bl\lp{t).

Вообще, если функция ]&гя]5 (t) пересекает О только в отдельные моменты времени, как, например, показано на рис. 16.2а, то тогда/-я составляющая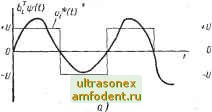

uf(t)

определено б)

. Рис. 16.2: а) Случай, когда иЩ хорошо определяется функцией sign ftfij) {t) ; б) Случай, когда и* (Q не полностью определяется функцией sign ftfij) (t)

и* (t) выражается релейной функцией, знак которой определяется функцией переключения, представляющей собой линейное сочетание составляющих сопряженного вектора я]5 (t).

Если для какого-то индекса i скалярное произведение тож-

дественно равняется нулю на конечном интервале времени, как показано на рис. 16.26, то имеем щ (t) = sign О и функция управления не определяется. Таким образом, принцип максимума не обеспечивает получения достаточной информации для решения задачи, и приходится обращаться к другим источникам информации.

В гл. 14 было показано, что L-управляемыми являются такие системы, в которых ни одна составляющая функции переключения Bijp (t) не равняется нулю на конечном интервале времени. Таким образом, мы видим, что /--управляемые системы не могут иметь вырожденных оптимальных по быстродействию решений.

Можно легко определить, почему системы, не являющиеся L-управляемыми, в состоянии давать вырожденные управления, как это видно из следующего примера.

Пример 16.3. Рассмотрим систему второго порядка, которая в канонической форме определяется выражением

Очевидно, что как система второго порядка она полностью управляема, но не L-управ-ляема. Предположим, что % действительны: далее примем 0> Jij Ji-s, а также Ui 1 и I 2 I 1. Рассмотрим теперь начальные состояния на линии х, (0) Х2 (0). Системы, включающие в себя х, и Х2, будут рассмотрены отдельно. Так как каждая система первого порядка L-управляема, то имеется единственное релейное оптимальное по быстродействию управление.