

 |
 |
|
Главная страница Системы автоматического управления Построение фазовых траекторий консервативной системы весьма наглядно. Чтобы убедиться в этом, следует прежде всего построить функцию P(xi)= f fix)dx В зависимости от Xi. Тогда, переписывая уравнение (4.38) в виде ха = ± [£ - р (Xl)] , нетрудно заметить, что для каждого значения £ можно построить зависимость Xg от Xl и, следовательно, траекторию системы. Пусть Р (Xi) определяется из графика, приведенного на рис. 4.23, а, где - р , Рч-r-f~P минимальное значение Р. Прежде всего отметим, что величина полной энергии Е не может быть меньше Piin- Если £=Pjj n, то для Ха существует единственное решение Xg = О, и, следовательно, значение Xl, при котором Р (Xi) = = Ptnmy является положением равновесия (точка Xig на рис. 4.23, б). llycTb Е хотя бы незначительно превосходит Ptnin. тогда существуют траектории, при движении по которым кинетическая энергия положительна. Поскольку кинетическая энергия пропорциональна xl, то траектория системы представляет замкнутую кривую, симметричную относительно оси Xl (кривая а на рис. 4.23, б) соответствует полной энергии Е - Е, рис. 4.23, а). Заметим, что условию Р (Xi)=£i удовлетворяют два значения координаты Xl, обозначенные через Хц и Xig. Они определяют предельные отклонения координаты Xl от положения равновесия, когда полная энергия равна Е. Поскольку Xl = Xg, то направление движения изображающей точки по траекториям определить нетрудно; на рисунке они отмечены стрелкой. В заключение сделаем вывод о том, что минимум потенциальной энергии соответствует положению равновесия, которое имеет сходство с центром. Теперь допустим что Р (Xi) = £4 и £4 > Е. Это значение полной энергии сответствует локальному максимуму функции Р (Xi) (рис. 4.23). Состояние Хае, где Р (Хае) == 4. является положением равновесия. Если Е чуть меньше £4, скажем, равно Е, то нетрудно прикинуть, что фазовый портрет вблизи точки Xi = Хае; Ха = О изображается кривыми е и г (рис. 4.23, б). Эти кривые не проходят через точку Хае, поскольку условие Р (Xi) = £3 определяет интервал (Xig, Х14), внутри которого отсутствуют траектории системы. Следовательно, состояние (Ха, 0), можно сопоставить с седловой точкой. Траектория, проходящая через точку (Хае, 0) обозначена буквой д. Аналогично можно показать, что точка перегиба функции Р (Xi) с горизонтальной касательной также соответствует положению равновесия. В этой точке Р (Xi) = Е, и соответствующая фазовая траектория обозна- 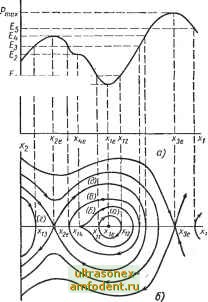 Рис. 4.23. Графический способ построения фазового портрета для консервативной системы: а зависимость Р = Р (ж,); б фазовый портрет чена буквой б. Итак, если график Р (л;1)для консервативной системы построен, достроить фазовую траекторию не представляет труда. Мы предлагаем читателю убедиться в правильности построения кривых на рис. 4.23, б. Результаты проведенного анализа сформулируем в виде следующей теоремы. Теорема 4.2. (Ж- Л. Лагранж). В консервативной системе шторого порядка, удовлетворяющей уравнениям = х, = -f (Xi), положения равновесия находятся в точках, для которых потенциальная энергия - P{.xi) J f{x)dx, как функция Xi соответствует либо локальному минимуму, либо точке перегиба с нулевым наклоном касательной. Траектории системы вблизи положения равновесия не расходятся от него только в том случае, если этой точке соответствует локальный минимум потенциальной энергии. Нетрудно показать, что только такое положение равновесия устойчиво, остальные неустойчивы. Это положение будет строго доказано в следующей главе. 4.6. ПОСТРОЕНИЕ ФАЗОВЫХ ТРАЕКТОРИЙ Поскольку решение дифференциального уравнения, соответствующего линейной автономной системе, всегда можно найти, то по этим решениям нетрудно построить и фазовые траектории системы. Для общего же случая нелинейных автономных- систем (не консервативных) следует искать новые способы. Рассмотрим систему вида Xi = fl (Xi, хУ, х = (Xi, Xs). (4.39) Ниже кратко исследукэтся различные способы построения фазовых траекторий для этой системы. 1. Отыскание фазовых траекторий на основе решения дифференциальных уравнений Если уравнение (4.39) удается решить непосредственно, то полученное решение определяет параметрическое задание траектории. Этот метод не требует комментарий. Иногда оказывается проще вместо интегрирования исходной системы проинтегрировать дифференциальное уравнение первого порядка, полученное в результате исключения времени, а именно: Если уравнение (4.40) удается проинтегрировать, то в рузультате получим аналитическое выражение для траекторий в функции фазовых координат. 2. Отыскание траекторий с помощью аналоговых и цифровых вычислительных машин Если указанные выше дифференциальные уравнения не удается решить аналитически, то часто это возможно сделать с помощью вычислительных машин. Аналоговый вычислитель и координатор для построения кривых Б плоскости {X -Y) может оказаться весьма гибким средством для решения поставленной задачи. Но даже в том случае, когда инженер может воспользоваться вычислительной техникой, он может внести ошибки в процессе программирования. Поэтому мы остановимся лишь на ряде тех методов, которые позволяют быстро оценить правильность решений, выданных вычислительной машиной. 3. Метод изоклин Рассмотрим систему (4.39), и пусть mfv v\- hi4 Ч) (4.41) По определениюm (Xi, ха) характеризует наклон касательной к траектории в точке (Xi, Ха). Тогда метод изоклин заключается в построении целого поля касательных в предположении, что в малой окрестности рассматриваемой точки ее наклон постоянен. После этого можно без труда построить траектории. Простейший способ построения поля касательных заключается в том, чтобы отыскать линии, соответствующие определенному наклону m касательной к искомой траектории. Чтобы проиллюстрировать сказанное, рассмотрим следующий пример. Пример 4.6. Голландский математик Балтазар Ван-дер-Поль при изучении одного класса осцилляторов показал, что их поведение можно описать уравнением 1 = 2; = -IИ -02 -1. (4.42) Теперь это уравнение обычно называют уравнением Ван-дер-Поля Для этой системы имеем Сходящиеся траектории Предельный цикл 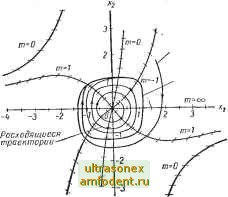 Рис. 4.24. Построение фазового портрета по методу изоклин для системы примера 4.6 = -fx(i-l)- ИЛИ, записывая относительно получим Пусть (X = 0,2, тогда кривая для m = О определяется уравнением =0.2(1-.)- Теперь требуется построить ее на фазовой плоскости. В точках этой линии проводим отрезки горизонтальных прямых, определяя тем самым направление фазовых траекторий (рис. 4 24). Кривая для т= -1 будет определяться уравнением =---г. В точках этой 1,2 - 0,2л; J кривой проводим короткие отрезки с наклоном -1. Продолжая этот процесс, получим поле касательных, как показано на рис. 4.24. Из построения видно, что вблизи начала координат траектории раскручиваются, но в конце концов оказывается, что они стремятся к замкнутой траектории, или предельному циклу. Траектории, начинающиеся вне области, ограниченной предельным циклом, также со временем сходятся к нему. Таким образом, при выбранном значении (х система имеет устойчивый предельный цикл.
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |