Составляющие вектора Ь, соответствующие k-v., {k + k-ii, . . ., > (Jj kiyu позициям, равны единице, а все остальные - нулю..

Блок-схема, соответствующая каждой из подматриц /ft. (Х), показана на рис. 2.8 (су, ki - вычеты).

3,kl

Рис. 2.8. Структурная схема линейной стационарной системы, матрица Л которой имеет жорданову форму Aj

Уравнения состояния, матрица А . которых или диагональная Л из собственных значений, или жорданова Aj, будут называться каноническими уравнениями состояния. В этом случае система представляется в простой форме, удобной для последующих выкладок.

2. Метод простых множителей

Если функция G (р) разложима на множители, ее можно представить в виде

G(p) = n

(2.27)

Соответствующая блок-схема показана на рис. 2.9. Принимая в качестве переменных состояния указанные на этом рисунке переменные, имеем

= Xii + и;

Рис. 2.9. Структурная схема линейной стационарной системы, функция G (р) которой разложейа на множители

(2.28)

причем выходной сигнал равен л: . При записи уравнений состояния в матричной форме соответствующие матрицы имеют вид

. . . О О

1 К . 1

(2.29)

(2.30)

Как нетрудно видеть, применимость этого метода не ограничивается случаем простых корней.

3. Метод, применяемый при аналоговом моделировании

При аналоговом моделировании система G (р) = ТЩ Риуется

различными обратными связями. При этом используются суммирующие, инвертирующие и интегрирующие звенья. Уравнения состояния можно записать, основываясь на этом представлении системы. В данном случае раскладывать L (р) на множители нет необходимости. Пример 2.5. Возможная реализация функции

У 1

(2.31)

показана на рис. 2.10. Если в качестве переменных состояния принять переменные, приведенные на рис. 2.10, то уравнения можно записать в виде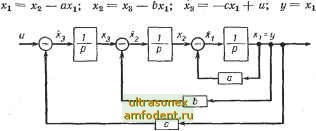

Рис. 2.10. Блок-схема аналогового моделирования объекта, описываемого уравнением (2.31)

Следовательно

4. Нормальная форма

Классический подход заключается в том, что в качестве переменных состояния принимаются выходной сигнал и п - 1 его производных. Преимущество такого подхода - простота представления результатов, когда собственные значения различны. Кроме того, как мы уже видели ранее [см. уравнение (2.2)1, такое представление возможно для нелинейного дифференциального уравнения общего вида. Если п = 2, то выходной сигнал может быть представлен классическим фазовым портретом на фазовой плоскости; более подробно это рассматривается в гл. 4. Если п > 2, выходной

сигнал может быть представлен траекториями в п-мерном фазовом простран-

стве *. Выбирая при L (р) = S л-хР в качестве переменных состояния

= у, x = Xi, Xg = X2, ... ; л; = а; 1, получим для уравнений состояния следующую матрицу:

о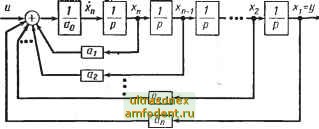

Рис. 2.11. Блок-схема аналогового моделирования объекта, уравнение которого записано в нормальной форме

В матричном уравнении имеем

Следуя Заде и Дезоеру [206], будем называть эти переменные нормальными переменными состояния.

При аналоговом моделировании система представляется, как показано на рис. 2.11.

2.5. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ С ЧИСЛИТЕЛЕМ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ПОРЯДКА I,

ГДЕ 1ги

Если числитель М (р) передаточной функции имеет порядок, меньший или равный порядку L (р), то система по-прежнему может быть описана уравнениями (2.18), (2.20).

* По этой причине некоторые авторы называют выбранные таким образом переменные состояния фазовыми координатами. Однако мы не будем здесь применять эту терминологию.