Применяя модифицированное г-преобразование с опережением * к выражению (8.27) и используя соотношение (8.28), получим

il (2, /и) =

i I 4 Л-Чо\ /Тат \

2 - е

-\г-~е 2JH-(2-

1)( + л:зо)Х

ДЛЯ. О <

(8.29а)

1 (Z, /п) =- ----2-{[Га(1-т)Н-1]2 +

+ 1-

-аТт

X- + (f/ + хзо) ДЛЯ 4ггп<1.

(8.296)

г- I

Чтобы функция 1 (z, m) была аналитической в области z 1, нужно члены вида - приравнять нулю. Тогда получим

Чо -

(8.30)

Из соотношения (8.30) видно, что предел в выражениях (8.29а) и (8.296) при г -> 1 существует. Используя соотношения (8.24), получим

Уп {тТ) = Хю + и

\ - аТт--т(] -2т)

(тГ) = { (1 -т) - [Та (1 - т) + 1]- 1

2Ue

,-аТт е

аТ 2 1

:т< 1.

(8.31)

При г (t) = R, используя выражения (8.31) и (8.13а), получим следующие условия переключения:

4/п (0) = - е = - t/ (аГ);

V + (аТ),

4-2-)

(8.32)

(8.33)

* При взятии модифицированного z-преобразования с опережением следует воспользоваться теоремой сдвига [см. соотношения (11.12) и (11.13) в приложении II].

Из выражений (8.32) и (8.33) следует, что

(8.34)

(8.35).

Заметим, что можно всегда найти величину Хю, которая будет удовлетворять выражению (8.34). Однако из графика функции t, (аТ), изображенного нарис. 8.5, определим

4g(aD аТ

<1 при аТ ф 0; = 1 при аТ = 0.

(8.36)

Отсюда видно, что для положительных г, U и а нельзя найти положительное Т, удовлетворяющее выражению (8.35). Таким образом, наше предположение неверно, и, следовательно, в такой системе колебания существовать не могут.

Пример 8.2. Рассмотрим теперь ту же систему, заменив отрицательную обратную связь положительной. Нетрудно видеть (рис. 8.1, 8.2, а), что это соответствует замене знака U в уравнении реле. Таким образом, подставляем и = -V; У> 0. Тогда выражение (8.35) приводится к виду

Этому условию можноудовлетворить, и, следовательно, при положительной обратной связи в системе могут существовать колебания. Однако при этом е> О, т. е. должен существовать гистерезис.

Пример 8.3. Рассмотрим систему с отрицательной обратной связью из примера 8.1, принимая а< 0. Из выражения (8.27) следует, что объект управления неустойчив, так как полюс s=-й>0. Это, в свою очередь, определяет полюс 2=1е~ >1 функции Ух (г, т) (8.29). Таким образом, чтобы сделать функцию (г, т) аналитической в области

Z 1 1, нужно не только исключить все члены вида --как это сделано в примере 8.1,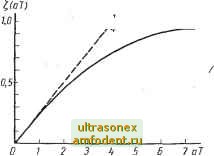

Рис. 8.5. График функции £ {аТ), построенный по выражению (8.33)

но и исключить все члены вида получим (упражнение 8.4)

2 -е

. Сделав это как в выражении (8.29а), так и в (8.296),

хзо = -Ut {аТ),

(8.37)

где S (аТ) - функция, определяемая соотношением (8.33). Условия (8.37) при этом удовлетворяются.

С учетом (8.37) функция (z, т) будет аналитической при z 1, и ее предел при Z -г- 1 существует. В результате снова получим выражение (8.31), как и в примере 8.1. Условия переключения (8.34) и (8.35) сохраняются теми же, что и для случая а<; 0. В заключение отметим, что условие (8.3 выполняется.

Имеем Z, (,-аТ) = -Q (аТ); если е > О и UO, то из выражения (8.35) следует, что величина Г > О может быть определена только при а<СО. Поэтому в системах управления двух последних примеров колебания могут существовать. Однако здесь снова должно выполняться условие е> О, т. е. нелинейность должна иметь гистерезис.

Как для примера 8.2, так и для примера 8.3 необходимые условия переключения (8.13а) выполняются. Для полной уверенности следует удовлетворять также условию (8.14 а). Последнее можно выполнить для конкретных численных величин, используя условие (8.31) (упражнения 8.2 и 8.5).

Заметим, что в примерах этого раздела возникающие в системах колебания не зависели от постоянного выходного сигнала R. Это обусловлено полюсом передаточной функции G (s) в точке s = 0. Интегрирующее свойство

объекта приводит к симметричным колебаниям т. е. = 2 ) следовательно, и {t) и е (t) в установившемся состоянии имеют нулевое среднее значение. А это значит, что установившаяся средняя величина выходного сигнала у (t) должна иметь постоянную величину, равную R, иначе говоря, в установившемся состоянии выполняется условие

У it) = R; (8.38)

это свойство было использовано в гл. 7, когда рассматривались колебательные сервомеханизмы с реле.

Установим теперь полезное соотношение, которое связывает выражение (8.24) с рядом Фурье. Это соотношение будет использовано в следующем параграфе при изучении метода Цыпкина.

Сделаем следующие предположения о свойствах передаточной функции G (s) и реакции объекта К о (s) на начальные условия:

1) функция h (t) = g (т)Л непрерывна при О оо;

2) функция у о (f) также непрерывна при О оо;

3) передаточные функции G (s) и Yq (s) не имеют особенностей при s =

= ±/ ; п = 1, 2, 3,. . ., но могут иметь полюс в точке s = 0. Из выражений (8.24) и (11.28 а) приложения П получим

у {тТ) = - S ri(/coon)e/2 , пфО, (8.39)*

п=-са

А 2Я

Подставляя выражение (8.21) в (8.39) и учитывая условие 3), имеем

г/ (тТ) = Уо + S 1 G{]щп)ei, пфО, (8.40)

гг=-оо

где Уо - среднее значение сигнала у (тТ), определяемое соотношением Ко = = lim iTsYo (s) + (s) G (s)]. (8.41)

Если функции G (s) и Уо (s) имеют полюсы при s = О, то колебания в системе симметричные, т. е. средние значения выходного сигнала реле и (t) я его входного сигнала е [t) равны нулю. Таким образом (см. рис. 8.1), среднее значение выходного сигнала системы у [t) должно быть равно

г (f), если G (s) не имеет полюса при s = 0:

Уо = г (t), если G (s) имеет полюс при s = 0.

где соо=

У it) =

* Из выражений (8.19а), (8.21) и предположений о виде передаточных функций G (s) и Fq (s) можно определить функцию (t) = S [Y (s)] [см. выражение (8.20)]; эта функция также непрерывна при 0<; t<oo.

Поэтому при т> О членом [у (тТ * ) - у (тТ)] можно пренебречь.

Таким образом, из выражения (11.28а) приложения II видно, что формула (8.39) справедлива во всем интервале О < m <; 1.

Из выражения (8.22) следует, что периодическая функция у {() непрерывна, поэтому формула (8.39) справедлива для произвольных значений т.

** Если G (s) имеет полюс при s = О, то (s) также имеет полюс.