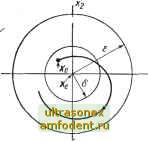Рис.

5.1. Устойчивость Ляпунову:

положение равновесия устойчиво, если для любого е > о найдется б > О, такое, что траектория, которая начинается в 6-окрестности х, все время остается в е-окрестности х

Ляпунова, следует для всякого, выбранного им наугад, е подобрать такое б, которое определяет окрестность начала координат и притом такую, что, находясь в ней в начальный момент времени, изображающая точка никогда не покинет выбранную е-окрестность. Это положение иллюстрируется с помощью рис. 5.1

Пример 5.2. Для линейной стационарной системы второго порядка, характеризуемой парой чисто мнимых полюсов, начало координат устойчиво в смысле Ляпунова, поскольку траектории свободного движения представляют замкнутые кривые, максимальное расстояние которых от начала координат определяется только начальными условиями и, в частности, зависит от наименьшего расстояния кривой откачала координат *. Следовательно, если выбрать произвольное е, например е, то тем самым мы зададим максимальное удаление траекторий от начала координат, но тогда величина б должна быть меньше, чем минимальное расстояние кривой от начала координат. Выбранное таким образом 6 будет удовлетворять определению устойчивости.

Пример 5.3. Обратимся вновь к уравнению Ван-дер-Поля. Положение равновесия, находящееся внутри области предельного цикла, неустойчиво в смысле Ляпунова, поскольку какую бы е-окрестность внутри области, ограниченной траекторией предельного цикла от начала координат, мы ни взяли, нельзя найти величины б, удовлетворяющей условиям устойчивости.

Анализ таких положений равновесия, как устойчивый фокус или узел, к которым сходятся все траектории, позволяет дать более узкое определение устойчивости с учетом асимптотического поведения. Это определение по-прежнему связано с малыми отклонениями от положения равновесия.

Определение 5.2. Состояние равновесия свободной динамической системы асимптотически устойчиво, если оно устойчиво и существует такое Ьа, что всякое движение, начинающееся из бд-ок-рестности положения равновесия Хе, стремится к нему при / оо. Если выполняется лишь однО второе условие, то говорят, что положение равновесия характеризуется квазиасимптотической устойчивостью.

Отметим, что по определению, прежде чем говорить об асимптотической устойчивости, нужно установить свойство устойчивости. Это необходимо для того, чтобы исключить из рассмотрения те случаи, когда траектории сначала отходят на произвольные сколь-угодно большие расстояния от положения равновесия, а затем начинают приближаться к нему. Отметим также, что указанное определение требует, чтобы траектории, начинающиеся достаточно близко от Xg, к тому же и стремились к Хе при / оо (рис. 5.2.). А. М. Ляпунов определил также условия, при которых система неустойчива.

Определение 5.3. Положение равновесия Хе свободной динамической системы неустойчиво, если существует такое е, что необходимого б.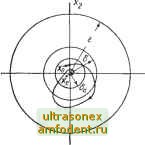

Рис. 5.2. Асимптотическая устойчивость:

положение равновесия х асимптотически устойчиво; если в дополнение к условиям устойчивости существует такое б что все траектории, начинающиеся в б-окрестности х

* В данном случае наименьшее расстояние от траектории до начала координат определяется величиной начальной скорости при нулевом значении координаты положения (Прим. ред.).

удовлетворяющего условиям определения 5.1, подобрать нельзя. Это определение достаточно очевидно. Отметим однако, что траектория неустойчивой системы всегда уйдет из любой наперед заданной окрестности начала координат, но это вовсе не означает, что такая траектория удалится бесконечно далеко от лг. Таким образом, начало координат в уравнении Ван-дер-Поля неустойчиво независимо от того, насколько мал предельный цикл.

Нельзя не отметить, что определения Ляпунова свойств устойчивости и асимптотической устойчивости - это локальные понятия, так как

они определяют устойчи-

-e(t)

,r(t) = 0 e(t)

u(t)

Рис. 5.3. Структурная схема управления примера 5.4

вое движение лишь в малом или в малой окрестности начала координат. Отметим также, и на это уже указывалось ранее, что величина е-окрестности несущественна, а определяющим фактором служит

б-окрестность. Если найдено б, удовлетворяющее условиям .устойчивости при выбранном Bj, то это же самое б удовлетворяет и определению для всех 8 > Ej. Поэтому следует выбирать лишь малые е и по ним отыскивать б *.

В дальнейшем мы будем говорить об устойчивости в малом и асимптотической устойчивости в малом, имея в виду данные нами определения устойчивости и асимптотической устойчивости по Ляпунову.

Следует отметить, что анализ устойчивости относительно произвольного положения равновесия можно заменить анализом другой системы, полученной в результате введения переменной л:-- х, относительно начала координат. Без ограничения общности всюду, в дальнейшем, будем изучать устойчивость системы относительно начала координат, если не сделана иная оговорка.

Рассмотрим несколько примеров.

Пример 5.4. Пусть имеем систему, показанную на рис. 5.3. Ее фазовый портрет в координатах (е, е) приведен на рис. 5.4. Для этой системы все траектории, которые начинаются в области

Уе2 -f е2 1,

(5.1)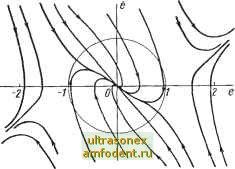

Рис. 5.4. Часть фазового портрета для системы управления примера 5.4

стремятся к началу координат. Более того, для всякого е можно найти 6, чтобы удовлетворить условиям Ляпунова. Отсюда следует, что начало координат асимптотически устойчиво.

Отметим, однако, что траектории, начинающиеся вне области, задаваемой уравнением (5.1), могут уходить и в бесконечность, как показано на рис. 5.4. В этом случае начало координат неустойчиво в большом. Такой результат нельзя получить, изучая лишь поведение траекторий в окрестности положения равновесия. Это обусловлено существованием других - неустойчивых состояний равновесия. Все станет яснее, когда мы подробно проанализируем эту систему в § 5.4.

Из сказанного следует, что анализ устойчивости в малом таит опасности, но в то же время именно этот тип устойчивости можно исследовать, используя столь распространенный в инженерной практике метод линеари-

* Из определения устойчивости также следует, что 6, соответствующее данному е, должно -быть меньше или равно е.

зации. В следующем параграфе метод линеаризации исследован подробно; установлена его связь с анализом устойчивости и даны некоторые обобщения.

Важный вопрос устойчивости в большом обсуждается в § 5.9 и детально излагается в гл. 9-И.

5.3. ЛИНЕАРИЗАЦИЯ

При решении задач анализа и синтеза всегда прибегают к линеаризации. Например, рассчитывая ламповый или полупроводниковый усилитель, линеаризуют его характеристику вблизи рабочей точки для определения параметров, влияющих на коэффициент усиления. Этот метод называют иногда методом возмущений.

В этом параграфе мы подробно изложим процесс линеаризации. При линеаризации системы оказывается возможным воспользоваться для анализа устойчивости первым методом Ляпунова, которому посвящается следующий параграф. Для того чтобы уяснить существо метода, рассмотрим Б качестве примера систему первого порядка.

Пример 5.5. Для системы х = -sin х состояния равновесия расположены в точках с координатами х = лп, и = О, 1, ... Непосредственное интегрирование определяет следующее решение:

tg-- = tg е-

из которого следует, что состояния х = 2тя, m = О, 1, ... устойчивы, в то время как состояния Xg= {2т-\- I) л, т= О, 1, ... неустойчивы. Этот результат, конечно, можно установить, изучая лишь фазовый портрет системы. Тем не менее сначала линеаризуем систему относительно начала координат и проследим последовательность действий, которая приводит нас к цели.

Предположим, что при t = to вследствие какого-либо возмущения состояние системы X {t) отклоняется от равновесного х на величину бх {t). Имеем

x{f) = Xe + Ьх (О для t> to. (5.2)

Это означает, что для рассматриваемой системы d

{Хе -Ь 6x) = - sin (Xg -I- 6л:). (5.3)

Правая часть уравнения (5.3) может быть представлена в виде ряда Тейлора относительно положения равновесия х, т. е.

{Xe + bx) = -smx + -{~smx)\ Ьх-]----=

- - sin Xg - cos Xg6x (5.4)

где члены второго порядка и выше в явном виде не выписаны.

Следует ожидать, что при достаточно малых Ьх поведение системы вблизи х можно описать уравнением (5.4), пренебрегая членами более высокого порядка, т. е.

{Xg -f 6x) != - sin - cos xx. (5.5)

Вычитая из этого уравнения тривиальное решение = -sin Xg, которое выполняется для положения равновесия, получим

d Д .

6х = 6л яа! - cos Xg6x; (5.6}

это и есть линеаризованное уравнение движения относительно возмущения 6х. Заметим, что когда Xg= О или 2тя, т = I, . . ., уравнение (5.6) сводится к виду бл = -6х, и асимптоти-